Modellierung und Modellbildung

…am Beispiel unserer Modellierstudie: „Identifizierung von verschiedenen Faktoren, die mit Covid-19 Todesfällen in Europa während der ersten Pandemie-Welle assoziiert sind“

Eine große Gruppe statistischer Verfahren, die der Erklärung vergangener und auch der Vorhersage künftiger Daten dienen soll, ist die Modellbildung oder statistische Modellierung. Damit meint man, dass man für einen gegebenen Datensatz mit sehr unterschiedlichen Variablen eine mathematische Struktur findet, die diesen Datensatz möglichst gut abbildet, zunächst einmal rein formal. Dieses Verfahren kann man nützen, um den Einfluss verschiedener Variablen auf eine Ergebnisvariable zu untersuchen. In der Sprachregelung der Modellbildung ist die Variable, die man erklären will, die abhängige Variable oder das Kriterium oder die Ergebnisvariable (Outcome), und die verschiedenen Variablen, die zur Aufklärung dieser einen Variable beitragen sollen, sind mehrere unabhängige Variablen oder auch Prädiktoren.

Ich verwende unsere eben publizierte Modellierstudie [1] als konkretes Beispiel. Sie wurde von mir konzipiert, ich habe erste Analysen gerechnet, dann stieg mein Kollege Rainer J. Klement ein, der als Physiker wesentlich flinker im Umgang mit solchen Modellen ist als ich.

In dieser Studie haben wir die Todesfälle der Menschen, die an Covid-19 in der ersten Welle der SARS-CoV2 Pandemie 2020 gestorben sind als abhängige Variable (Outcome, Ergebnisvariable oder Kriteriumsvariable) verwendet. Wir wollten wissen: Welche Einflüsse auf diese Variable sind besonders wichtig, welche eher vernachlässigbar, und wie viel der Schwankungsbreite können wir mit den Variablen, die wir als Prädiktoren ausgesucht haben, erklären. Technisch spricht man dabei von der Aufklärung von Varianz dieser Ergebnisvariable. Oder, nochmals anders ausgedrückt: Welche Einflüsse tragen zu den Schwankungen der Covid-19 Todesfälle in den verschiedenen europäischen Ländern bei?

Dass die Todesfälle an und mit SARS-CoV2 nicht einfach durch das Virus allein erklärbar sind, zeigt schon die simple Tatsache, dass die auf Bevölkerung standardisierten Sterberaten in allen europäischen Ländern sehr unterschiedlich sind. Wäre das Virus allein die Ursache dafür, dann müssten auf 100.000 Personen standardisierte Sterbezahlen zu einem Stichtag etwa gleich groß sein. Das sind sie nicht. Das wurde recht schnell klar. Ebenfalls klar geworden ist rasch, dass es eine Vielzahl anderer Gründe für die unterschiedlichen Covid-19-Todesraten in einem Land geben muss, außer dem Virus. Denn, kleines Beispiel: Belgien, das eine Grenze mit Deutschland hat, hatte in der ersten Welle die mit Abstand höchsten Covid-19-Todesraten und Deutschland mit Abstand die kleinsten. Wären alle Todesfälle ausschließlich auf das Virus zurückzuführen und wäre die SARS-CoV2 Epidemie die einzige Ursache für Todesfälle, dann müssten die Todesfälle in beiden Ländern – immer auf die gleiche Anzahl von Menschen gerechnet – gleich hoch sein. Denn ein Virus lässt sich nicht von einer Grenze aufhalten, zumal alle „Maßnahmen“ sowieso zu spät kamen.

Das also ist die Motivation für diese konkrete Modellierstudie. Für alle Modellierungen im Allgemeinen gilt: Wir beobachten Schwankungen, technisch gesprochen Varianz, in einem bestimmten Parameter oder in einer bestimmten Variablen, in diesem Falle in der Zahl der Covid-19 Todesfälle pro Land. Wir wollen wissen, wie diese Schwankung zustande kommt. Anders ausgedrückt: Wir wollen wissen, welche möglichen Variablen an dieser Schwankung beteiligt sind oder welche Variablen einen Einfluss darauf haben.

Wer das Grundprinzip der Modellierung nicht kennt, könnte sich vorab meinen Methodenblog zum Thema „Modellierung“ ansehen. Dann ist leichter verständlich, was wir in dieser Modellierstudie gemacht haben, in der wir versucht haben zu verstehen, welche Variablen einen Einfluss auf die Variation der Covid-19 Todesfälle in der ersten SARS-CoV2-Welle Anfang 2020 haben.

Die Modellierung von Variablen, die Covid-19 Todesfälle in Europa möglicherweise beeinflussen

Unsere Kriteriums- oder Zielvariable war also die Rate der Covid-19 Todesfälle in jedem europäischen Land während der ersten Welle der SARS-CoV2-Pandemie. Wir verwendeten die Daten von 43 europäischen Ländern zum Stichtag 20. August 2020. Dieser Tag war der Tag, an dem die erste Welle so ziemlich überall vorüber war und wurde einigermaßen pragmatisch gewählt. Wir verwendeten die bis dorthin gezählten Todesfälle, die Covid-19 zugeschrieben wurden, aus der öffentlich verfügbaren Datenbank, wie sie die Webseite „Our World in Data“ (OWID) anbietet.

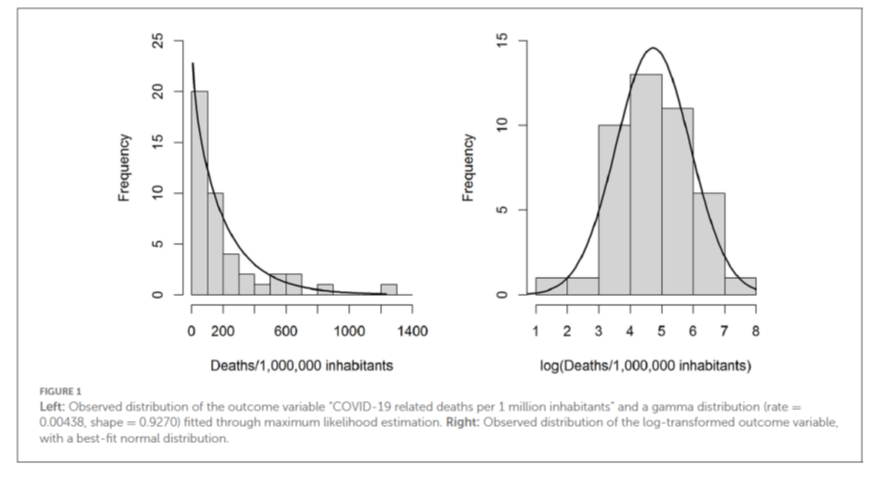
Die Verteilung dieser Variablen ist nicht normalverteilt, sondern folgt einer Gamma-Verteilung relativ genau (siehe Abbildung 1, links). Führt man eine logarithmische Transformation dieser Variablen durch, dann folgt sie einigermaßen brauchbar einer Normalverteilung (Abb. 1 rechts).

Wir wählten daher einen doppelten analytischen Ansatz, wobei der erste im Protokoll als Hauptanalyse formuliert wurde, der zweite als Sensitivitätsanalyse.

Protokoll

Protokolle sind übrigens Projektbeschreibungen, in denen die wichtigsten Auswertungs- und Analyseschritte definiert werden, bevor irgendwelche Auswertungen durchgeführt werden. Ich formuliere standardmäßig immer Protokolle und stelle sie vor Beginn einer Untersuchung öffentlich zur Verfügung, meistens auf der Open Science Foundation Plattform. Bei klinischen Studien ist dies seit einiger Zeit Standardvorgabe und dort werden Protokolle in entsprechenden Studienregistern in einer Datenbank geführt (z.B. clinicaltrials.gov), damit man sich am Ende davon überzeugen kann, dass sich die Autoren an die Vorgaben hielten. Auch in diesem Fall habe ich ein Protokoll erstellt (https://osf.io/x93np/; dort befindet sich auch ein Update und ein Analyseskript). Mittlerweile haben sich einige Verbesserungen ergeben, die wir in der Publikation erwähnt haben.

Analytische Strategie

In diesem Fall diente uns die Modellierung, um zu verstehen, ob und welche Variablen einen Einfluss auf die Todesraten haben. Daher formulierten wir unterschiedliche Modelle mit unterschiedlicher Komplexität. Wir rechneten generalisierte lineare Modelle auf eine gamma-verteilte Kriteriumsvariable. Solche Modelle kann man verstehen wie einfache lineare Modelle, mit dem Unterschied, dass die Variablen nicht mit einem einfachen additiv-linearen Link verbunden sind, sondern als logarithmische Funktion miteinander verknüpft werden. Weil sie etwas komplexer sind, kann man ihre Ergebnisse auch nicht einfach direkt interpretieren. Zwar kann man auch für sie einen R²-ähnlichen Kennwert, den sog. Kullback-Leibler R²-Wert errechnen, den man als Prozentsatz der aufgeklärten Varianz interpretieren kann. Aber damit die Daten leichter interpretierbar sind, haben wir auch ein lineares Modell auf eine log-transformierte Zielvariable gerechnet. Die Ergebnisse sind sehr ähnlich, was zeigt, dass die Modellbildung erfolgreich war.

Das einfachste Modell bildet die Hypothese ab: Ausschließlich die Fallzahlen (selbstverständlich standardisiert auf die Anzahl der Tests) sind für Todesfälle verantwortlich. Je mehr Fälle, umso mehr Tote. Weil diese Variable sehr schief verteilt ist, haben wir sie logarithmiert. (Dies ist übrigens eine Veränderung gegenüber meiner ursprünglichen Analyse und Beschreibung [2]. Logarithmiert man nämlich diese Variable, dann wird das Modell besser und die Varianzaufklärung steigt. Waren es mit den rohen Werten nur 7 % Varianzaufklärung, sind es mit den logarithmierten Werten 20 % Varianzaufklärung).

Maßnahmen

Eine weitere interessierende Variable ist der Einfluss der „Maßnahmen“, technisch „non-pharmaceutical interventions“ (NPIs), im Volksmund gerne „Lockdown“ genannt. In Wirklichkeit bestehen diese „Maßnahmen“ aus einem Bündel von möglichen Interventionen, von Schulschließungen, über Grenzschließungen, Ausgangssperren, Ladenschließungen, Maskenpflicht, Schließen von kulturellen Räumen und Restaurants, bis hin zur strikten Order zu Hause zu bleiben. Die Blavatnik-School of Policiy der Universität Oxford stellt einen Tracker zur Verfügung, der für alle Länder dieser Erde die Striktheit dieser Maßnahmen beschreibt in einem auf 100 % genormten Wert (0: keinerlei Maßnahmen; 100: maximal denkbare Maßnahmen). Dieser Wert ändert sich und wird wöchentlich adaptiert. In unserer Analyse taucht diese Variable als Government Response Severity Index (GRSI) auf, und zwar als mittlere Schwere in einem Land über den interessierenden Zeitraum.

Das zweite Modell stellte also die Wirksamkeit der politischen Reaktionen in den Vordergrund.

Grippeimpfungen, Vitamin-D-Status, Krankenhausbetten

Das dritte mögliche Modell verwendet neben der Fallzahl einige medizinische Variablen, nämlich den Prozentsatz der älteren Bevölkerung, der gegen Grippe geimpft ist. Das wurde motiviert durch eine interessante Studie, die einen positiven Zusammenhang zwischen Grippe-Impfung und Covid-19-Todesraten fand [3]. Wir nahmen in dieses Modell als möglichen Protektiv-Faktor, der durch verschiedene Studien erhärtet war, die Vitamin-D-Versorgung der Bevölkerung auf, die wir aus unterschiedlichen Studien zusammengestellt hatten, sowie die Anzahl der Krankenhausbetten auf 100.000 Einwohner.

Populationsparameter

Weil vor allem ältere Menschen von Covid-19 betroffen sind, formulierten wir ein Modell, in dem neben der Fallzahl und dem Vitamin-D-Status die Lebenserwartung in einem Land und die Anzahl der älteren Bevölkerung als Prädiktoren verwendet wurden.

Risikofaktoren

Risikofaktoren, wie koronare Herzkrankheit und Diabetes, sowie Rauchen als möglicher Risiko- oder gar Protektivfaktor [4, 5] gingen in ein weiteres Modell ein, zusätzlich zu Fallzahl und Vitamin-D-Status.

Länderspezifische Faktoren

Schließlich bildeten wir noch ein Modell, bei dem neben den log-transformierten, standardisierten Fällen und dem Vitamin-D-Status noch länderspezifische Faktoren wie Bevölkerungszahl und -dichte, Prozent der Alten, Bruttoinlandsprodukt und Entwicklungsindex eingingen.

Volles Modell und datengesteuertes Modell via LASSO-Analyse

Schließlich analysierten wir noch das volle Modell mit allen 13 Variablen und rechneten ein datengetriebenes Modell mit einer relativ neuartigen Analysemethode, die abgekürzt LASSO heißt [6]. LASSO ist eine Abkürzung für „Least absolute shrinkage and selection operator“, eingedeutscht: ein Operator, der die am wenigsten bedeutsamen Prädiktoren auf null setzt und diejenigen selektiert, die dann an Bedeutung gewinnen.

Das volle Modell ist einfach zu verstehen: Es verwendet einfach alle Variablen. Das LASSO-Modell ist datengesteuert. Hier werden in einem iterativen Verfahren alle Variablen auf null gesetzt, bis auf eine. Von diesen wird zunächst diejenige gewählt, die den gewichtigsten Beitrag zur Varianzaufklärung leistet. Dann wird dieser iterative Prozess für die nächsten übrig-gebliebenen Variablen wiederholt, usw. Dies ist zunächst ein rein exploratives Verfahren, das aber den Vorteil hat, dass es ohne eine multiple Modellbildung auskommt. Auf diese Art und Weise kann man erkennen, welche Variablen wirklich wichtig sind und formuliert dann für diese so ausgewählten Variablen ein Modell.

Auswahl der Modelle und das Akaike-Informationskriterium

Diese 8 Modelle ergeben unterschiedlich gute Anpassungen an die Daten. Wie entscheidet man nun? Hier hilft das sog. Akaike-Informationskriterium (AIC), das der japanische Statistiker Akaike vorgeschlagen hat. Es ist eine absolute und für sich genommen wenig aussagekräftige Zahl, in die die Anpassungsgüte eines Modells und die Anzahl der dafür notwendigen Parameter eingeht. Ein Modell mit größerer Parameteranzahl wird „bestraft“, indem das AIC ansteigt. Daher kann man das AIC verwenden, um die relative Modellgüte zu bestimmen.

Aus einer Klasse von Modellen ist dasjenige das Beste, das das vergleichsweise niedrigste AIC aufweist.

Wir haben die Analyseergebnisse und die entsprechenden Modellparameter in Tabellen 1 und 2 der Originalpublikation dargestellt.

Ich gebe hier in Tabelle 1 nur die wichtigsten Ergebnisse wieder.

Modell No und Variablen im Modell	Regressions-gewicht b	Signifikanz von b p-Wert	KL-R2	AIC	Delta AIC
Modell 1			0.2	541.3	36.2
Fälle	0.6	.0008
Modell 2			0.26	538.5	33.4
Fälle	0.6	.0005
GRSI	0.04	.035
Modell 3			0.47	524.8	19.7
Fälle	0.73	2*10-5
Vitamin D	-0.3	.4
Betten	0.025	.7
Grippeimpfung	0.032	3*10-5
Modell 4			0.45	527.5	22.43
Fälle	0.73	3*10-6
Vitamin D	-0.47	.11
Lebenserwartung	0.19	4 * 10-5
Anteil Alter	-0.033	.5
Modell 5			0.49	524.9	19.8
Fälle	0.71	8*10-5
Vitamin D	-0.36	.2
Raucher (%)	-0.007	.8
CVD Todesfälle	-0.999	.02
Diabetes Prävalenz	-0.09	.18
Modell 6			0.48	527.5	22.42
Fälle	0.96	6*10-6
Bevölkerungdichte	0.22	.058
Lebenserwartung	-0.011	.88
BPI	2.6*10-5	.09
HDI	1.94	.7
%Alte	0.08	.2
Modell 7			0.67	524.2	19.1
Fälle	0.97	2*10-6
GRSI	0.03	.055
Vitamin D	-0.716	.043
Grippe             Impfungsrate	0.02	.0055
Lebenserwartung	-0.05	.7
Bevölkerungsdichte	0.09	.4
%Raucher	-0.014	.5
CVD Mortalität	-0.04	.9
Diabetes Prävalenz	-0.06	.4
Betten	0.03	.6
BPI	4*10-8	.005
HDI	-2.5	.6
%Alte	0.09	.14
Modell 8			0.68	505.1	–
Fälle	0.84	9*10-7
GRSI	0.02	.07
Vitamin D	-0.7	.02
Grippe             Impfungsrate	0.02	.0002
Bevölkerungsdichte	0.13	.2
BPI	3*10-5	.007

Die lineare Regression auf die log-transformierte Kriteriumsvariable erbrachte wie gesagt fast die gleichen Ergebnisse, daher gehe ich darauf nicht ein. Wer mag, kann sich die Originaltabelle ansehen. Außerdem sei noch erwähnt: Wir haben fehlende Fälle durch einen Interpolationsalgorithmus ersetzt, weil wir nicht für alle Variablen für jedes Land Daten hatten und weil bei fehlenden Werten ein Fall von der Analyse ausgeschlossen wird, was die statistische Mächtigkeit reduziert. Um zu kontrollieren, ob diese Prozedur einen Einfluss hatte, haben wir die Analyse für die Daten angepasst, für die alle Fälle vorlagen und erhielten ziemlich die gleichen Ergebnisse; auch das stelle ich hier nicht extra dar. Die Tabelle befindet sich in der Originalpublikation.

Widmen wir uns nun den Modellen und was sie uns sagen. Beginnen wir mit dem schlechtesten und einfachsten, Modell 1, bei dem nur die standardisierte Fallzahl als Prädiktor verwendet wird. Dieses Modell testet die Hypothese, ob die Anzahl der Fälle als Prädiktor ausreicht. Offensichtlich ist das nicht der Fall. Sowohl die Modellpassung, erfasst durch das Akaike Informationskriterium, als auch die Varianzaufklärung sind am schlechtesten bei diesem Modell. Die Differenz des AIC zum besten Modell ist am größten, nämlich 36.2. Man geht in der Regel davon aus, dass AIC-Differenzen unter 5 in etwa gleichwertige Modelle signalisieren und über 15 ein Modell als unplausibel ausscheiden lassen.

Das beste Modell ist eindeutig das durch die LASSO-Regression gefundene datengestützte Modell Nummer 8. Es kann mit nur 6 Variablen mehr Varianz aufklären, nämlich 68 %, als das Modell, das alle Variablen nutzt, nämlich Modell 7. Dieses hat mit einer AIC-Differenz von 19.1 Punkten auch einen wesentlich schlechteren Wert. Das Gleiche gilt für alle anderen Modelle, die ich deshalb gar nicht erst diskutiere.

Die Anzahl der Fälle geht auch im besten Modell Nummer 8 als signifikanter und stärkster Prädiktor ein. Der zweitstärkste Prädiktor ist die Versorgung der Bevölkerung mit Vitamin D. Dieser Prädiktor ist negativ, also protektiv und signifikant. Die Daten zur Vitamin-D-Versorgung sind an sich schlecht, weil es wenig gute populationsgestützte Studien für alle europäischen Länder gibt. Daher haben wir die Variable dichotomisiert in ausreichend oder nicht-ausreichend. Das ist natürlich extrem grobkörnig. Umso erstaunter waren wir, dass wir trotzdem einen relativ starken Effekt gefunden haben. Wir haben die Analyse mit der geografischen Breite nachvollzogen und sahen, dass diese allein den Effekt nicht erklärt. Der Prädiktor, der als Drittes kommt, gemessen an der Größe des Regressionsgewichtes, ist die Bevölkerungsdichte: je größer, umso mehr Fälle. Allerdings ist dieser Prädiktor nicht signifikant, spielt also trotz seiner Größe eine untergeordnete Rolle.

Die Rate der Durchimpfung der älteren Bevölkerung mit Grippeimpfung ist ein hochsignifikanter Prädiktor, auch wenn der Einfluss eher klein ist: je mehr grippegeimpfte Alte in einem Land, umso mehr Covid-19-Todesfälle.

Wie lässt sich das verstehen? Zum einen ist denkbar, dass es noch immer Hintergrundvariablen gibt, die wir nicht erfasst haben, die diesen Einfluss treiben. Diejenigen, die wir erfasst haben, spielen darin jedenfalls keine Rolle. Denn die Variable ist selbst im vollen Modell, in das alle Variablen eingehen, ein signifikanter Prädiktor und in allen anderen Modellen, in denen wir sie eingebracht haben. Sie hängt univariat nur mit der Lebenserwartung zusammen (r = .56) und mit der kardiovaskulären Mortalität negativ (r = -.57), also je mehr Grippeimpfungen, umso weniger kardiovaskuläre Mortalität in einem Land. Aber: je mehr Grippeimpfungen, umso mehr Covid-19 Mortalität. Wir haben anscheinend die Wahl zwischen Pest und Cholera sozusagen. Gegen alles gleichzeitig scheinen wir uns nicht schützen zu können. Zum einen ist da das Phänomen, dass Erreger offenbar eine Art symbiotisches Ökosystem bilden. Vertreibt man einen, kommen eben andere. Zum anderen könnte es sein, dass die Impfung gegen Grippe das Immunsystem eine Weile beschäftigt. [7] In dieser Zeit hat es vielleicht ein anderer Erreger leichter, das Immunsystem zu überwinden. Eine sehr gute randomisierte Studie an Kindern zeigte: Gegen Grippe geimpfte Kinder hatten zwar deutlich weniger Risiko, an Grippe zu erkranken, aber ein vierfach gesteigertes Risiko, an anderen Atemwegsinfekten zu erkranken. [8]

Das Bruttoinlandsprodukt ist in diesem Modell ein typisches Beispiel für einen hochsignifikanten, aber sachlich wenig wichtigen Prädiktor, denn sein numerischer Wert ist extrem klein, nämlich 0,00003: je mehr ein Land erwirtschaftet, umso größer die Covid-19 Mortalität in diesem Land.

Am interessantesten aus konzeptueller Sicht ist für mich die Tatsache, dass der Government Response Index GRSI, der die Härte der Maßnahmen abbildet, ein zwar schwacher, aber positiver Prädiktor ist. D.h.: je stärker die Maßnahmen, umso mehr Todesfälle. Hätten die Maßnahmen in der ersten Welle irgendetwas Positives bewirkt, hätten wir hier ein negatives Vorzeichen erwartet. Genau das ist nicht der Fall. Zwar ist der Prädiktor auch nicht gerade sonderlich signifikant, spielt also auch keine große Rolle, aber wenn schon, dann eine unrühmliche. Wir hatten schon in einer anderen Publikation gezeigt, dass die unselige Modellierstudie, die angeblich belegt, dass Deutschlands Lockdown nötig war [9], eine falsche Datengrundlage verwendete [10]. Die Datenbasis für die Wirksamkeit von Lockdowns und Maßnahmen ist aus meiner Sicht schlecht. Diese neue Analyse erhärtet diesen Befund.

Zusammenfassung unserer Covid-19 Mortalitäts-Modellierung

Wir wissen jetzt also: in der ersten Phase der SARS-CoV2-Ausbreitung waren die Fallzahlen, standardisiert auf die Anzahl der Tests, ein wichtiger Prädiktor, der etwa 20 % der Varianz erklärt. Allerdings kann das beste Modell mit 6 Variablen insgesamt 68 % der Varianz erklären. Die Härte der Maßnahmen spielt eine Rolle: je härter die Maßnahmen, umso mehr Todesfälle; je dichter die Bevölkerung zusammenwohnt, umso mehr Todesfälle; je besser die Versorgung mit Vitamin D, umso weniger Todesfälle; je höher die Durchimpfungsrate mit Grippeimpfung bei den Älteren, umso mehr Todesfälle; je höher das BIP, umso mehr Todesfälle. Dabei bleiben 32 % der Varianz ungeklärt. Wir wissen, dass die berühmten Vorerkrankungsvariablen (Prävalenz von Diabetes, von kardiovaskulären Erkrankungen und von Rauchen) dabei keine große Rolle spielen; denn Modelle, in die wir diese eingebracht haben, sind weniger gut in der Aufklärung der Varianz. Aber es könnte natürlich sein, dass wir andere wichtige Variablen übersehen haben: wie glücklich ein Land im Durchschnitt ist, wie hoch das Angstniveau ist oder die Depressionsrate. Diese haben wir nicht überprüft. Das können andere gerne noch tun. Unser Datensatz steht zur Verfügung. Aber ich finde: 68 % Varianzaufklärung ist schon ganz schön gut. Und wenn man diese Information ernst nehmen würde und zum Beispiel eine flächendeckende Kampagne zur ausreichenden Vitamin-D-Versorgung der Bevölkerung durchführen würde, oder jedem Haushalt entsprechendes Material zur Verfügung stellen würde, dann wäre das garantiert effektiver als Maskenpflicht in Zügen und Schulen. Soviel kann man sagen. Denn die Maskenpflicht ist Teil des GRSI und der spielt eher eine unrühmliche Rolle.

Quellen und Literatur

1. Klement RJ, Walach H. Identifying factors associated with Covid-19 related deaths during the first wave of the pandemic in Europe. Frontiers in Public Health. 2022;6th July 2022. doi: https://doi.org/10.3389/fpubh.2022.922230.
2. Klement RJ, Walach H. Low Vitamin D Status and Influenza Vaccination Rates are Positive Predictors of Early Covid-19 Related Deaths in Europe – A Modeling Approach. Zenodo. 2021. doi: https://doi.org/10.5281/zenodo.4680691.
3. EBMPHET  Consortium. COVID-19 Severity in Europe and the USA: Could the Seasonal Influenza Vaccination Play a Role? SSRN. (7/6/2020). doi: https://doi.org/10.2139/ssrn.3621446
4. Patanavanich R, Glantz SA. Smoking is Associated with COVID-19 Progression: A Meta-Analysis. medRxiv. 2020:2020.04.13.20063669. doi: https://doi.org/10.1101/2020.04.13.20063669.
5. Farsalinos K, Eliopoulos E, Leonidas DD, Papadopoulos GE, Tzartos S, Poulas K. Nicotinic Cholinergic System and COVID-19: In Silico Identification of an Interaction between SARS-CoV-2 and Nicotinic Receptors with Potential Therapeutic Targeting Implications. International Journal of Molecular Sciences. 2020;21(16):5807. PubMed PMID: doi: https://doi.org/10.3390/ijms21165807.
6. Tibshirani R. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society B. 1996;58:267-88.
7. Cowling BJ, Nishiura H. Virus Interference and Estimates of Influenza Vaccine Effectiveness from Test-Negative Studies. Epidemiology. 2012;23(6):930-1. doi: https://doi.org/10.1097/EDE.0b013e31826b300e. PubMed PMID: 00001648-201211000-00030.
8. Cowling BJ, Fang VJ, Nishiura H, Chan K-H, Ng S, Ip DKM, et al. Increased risk of noninfluenza respiratory virus infections associated with receipt of inactivated influenza vaccine. Clin Infect Dis. 2012;54(12):1778-83. Epub 03/15. doi: https://doi.org/10.1093/cid/cis307. PubMed PMID: 22423139.
9. Dehning J, Zierenberg J, Spitzner FP, Wibral M, Neto JP, Wilczek M, et al. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science. 2020;369(6500):eabb9789. doi: https://doi.org/10.1126/science.abb9789.
10. Kuhbandner C, Homburg S, Walach H, Hockertz S. Was Germany’s Lockdown in Spring 2020 Necessary? How bad data quality can turn a simulation into a dissimulation that shapes the future. Futures. 2022;135:102879. doi: https://doi.org/10.1016/j.futures.2021.102879.