(25) Modelle und Kausalität

Können wir mit solchen Modellen etwas über Kausalität aussagen? Können wir zum Beispiel sagen, dass Grippeimpfungen die Covid-19 Todesraten kausal erhöhen, oder ein höherer Vitamin-D-Spiegel die Covid-19 Todesraten kausal senkt? In einem technisch-methodischen Sinne geht das nicht. Denn wir haben lediglich Querschnittdaten vor uns. Es ginge nur, wenn wir gleichzeitig ein starkes theoretisches Modell hätten. Wir können die umgekehrte Kausalität ausschließen: Covid-19-Todesraten treiben nicht die Impfquote bei Älteren in die Höhe (weil die Daten zu den Grippeimpfungen meistens aus der Zeit vor der Pandemie stammen), und wir können auch ausschließen, dass Covid-19-Todesraten den Vitaminspiegel senken. Denn dafür gibt es keine plausible Theorie. Denkbar wäre allerdings, dass Covid-19-Todesraten den GRSI treiben: Je mehr Todesfälle in einem Land, umso stärker reagiert die Regierung. Allerdings täuscht sie sich meistens in der Annahme, die Maßnahmen hätten was mit der Dynamik der Todesfälle zu tun. Eher andersherum: Die Dynamik der Maßnahmen wird von der Dynamik der Todesraten getrieben.

Das führt mich zu ein paar Überlegungen zum Thema Kausalität und wie man sie allenfalls im Rahmen von Modellierungen klären kann. Zunächst ein paar allgemeine Bemerkungen zum Thema Kausalität.

Kausalität

Die immer noch klügste und bislang unübertroffene Analyse der Kausalität stammt meines Erachtens von David Hume,[1] der sie im übrigens höchstwahrscheinlich von William Ockham hat [2, 3, S. 629] und wenn er sie dort nicht abgekupfert hat, dann war er einfach ein sehr schlauer Mann, der unabhängig etwa dasselbe Ergebnis erhalten hat.

Ockham hat in seinem Kommentar zur aristotelischen Physik, den er wohl während seiner Lehrzeit in Oxford zu Beginn des 14. Jahrhunderts geschrieben hat, Ursache folgendermaßen definiert: „Wir müssen einen Satz annehmen, der evident erscheint, und das ist folgender: ‚Das ist die Ursache einer anderen Sache: wenn sie nicht vorhanden ist – alles andere unverändert – ist auch die Sache nicht; wenn sie vorhanden ist, dann ist auch die Sache gegeben.‘“ [3, S. 629] Dies ist eine rein korrelative, negative Formulierung: Wenn die Ursache nicht vorliegt, liegt auch der infrage stehende Sachverhalt nicht vor. Wenn die Ursache vorliegt, ist auch der Sachverhalt da. Beispiel: Licht ist die Ursache des Sehens. Ist kein Licht da, sehen wir nicht. Ist es da, sehen wir. Oder: Wo kein Rauch ist, ist kein Feuer. Ist da Feuer, dann ist auch Rauch da.

Ockham hat im Zuge seiner Kritik an den scholastischen Konzepten alle Essenzen, Entitäten und Kräfte, die etwa Ursachen vermitteln würden, aus dem Weg geräumt und den Ursachenbegriff rein korrelativ formuliert.

Hume hat diese Analyse aufgegriffen, ob wissend oder nicht wissend ist an dieser Stelle gleichgültig. Hume analysiert „Ursache“ als ein mentales Konzept. Etwas, das wir der Welt überstülpen. Kausalität hat drei Voraussetzungen, eine davon hat auch Ockham analysiert: die Regelhaftigkeit des gemeinsamen Auftretens von Ursache und Wirkung. Dazu kommt lt. Hume noch: die zeitliche Reihenfolge und die räumliche Nachbarschaft.

Denn Ursachen gehen Wirkungen voraus. Und in aller Regel nennen wir nur das eine Ursache, das unmittelbare räumliche oder sachliche Nähe aufweist. Wenn jemand betrunken Auto fährt und dabei einen Fußgänger verletzt, dann würden wir im juristischen Sinne den Alkoholkonsum als die Ursache des Unfalls ansehen. Den Ärger, den der Fahrer vielleicht mit seinem Chef hatte und der ihn veranlasste, mit seinen Kumpels ein paar Bier mehr zu trinken, oder die Persönlichkeitsstruktur, die ihn für Alkoholkonsum anfällig macht, würden wir in diesem Sinne nicht als Ursache sehen. Denn diese sind die „ferneren“, die weiter weg liegenden Ursachen, die aber durchaus auch als Ursache infrage kämen.

Das Konzept einer „Ursache“ hat also durchaus auch einen gewissen willkürlichen Charakter. Wir nennen etwa in der SARS-CoV2-Epidemie das Virus eine Ursache von Todesfällen, obwohl, wie wir gesehen haben, nur 20 % der Varianz auf das Virus und die Infektion mit ihm zurückzuführen sind. Eigentlich könnten wir mangelnden Vitamin-D-Status mit viel größerer Berechtigung als Ursache anführen. Denn nur wer zu wenig Vitamin D hat erkrankt und kann dann in der Folge sterben. Vitamin-D-Mangel könnten wir im Prinzip leichter beeinflussen als die Ansteckung mit einem Virus verhindern. Warum tun wir das nicht? Nicht, weil es theoretisch zwingend ist, sondern weil wir gewohnt sind, so zu denken, und weil die Humesche Analyse nahelegt, dass wir in der Regel nur die zeitlich und räumlich naheliegenden Ereignisse als Ursache ansehen.

Vitamin-D-Mangel geht einer Infektion ebenfalls voraus und ist ebenfalls sehr eng mit ihr verbunden. Aber die konzeptuelle Distanz ist größer. Daher verwenden wir Vitamin-D-Mangel selten als Ursache.

Man sieht an dem Beispiel: Was wir als Ursache ansehen und was nicht, unterliegt auch einer gewissen Konvention. Ockham hat klar gesehen: nur die Regelhaftigkeit des Zusammenhangs ist ein hinreichender Definitionsgrund. Hume hat noch die zeitliche Reihenfolge nachgeschoben. Das ist irgendwie einleuchtend: nur was vorher war, kann eine Ursache sein. Aber schon bei räumlicher und zeitlicher Nähe wird es komplex.

Wir könnten vielleicht sagen: Wir benötigen ein theoretisches, konzeptuelles Verständnis für den Zusammenhang zwischen Ursache und Wirkung. Wir haben zwar ein einigermaßen gutes, aber in Details auch vages Verständnis zwischen Persönlichkeitsstruktur und Alkoholmissbrauch, oder zwischen sozialem Stress und Alkoholmissbrauch. Diese Kenntnis eignet sich dazu, retrospektiv zu verstehen, warum etwas so kam, aber nicht dazu, vorauszusagen, dass es so kommen wird. Denn die Zusammenhänge sind selten deterministisch. Da die Assoziation zwischen erhöhtem Alkoholspiegel und Fahruntüchtigkeit mit Sicherheit deutlich besser belegt ist, taugt sie mehr zu einem theoretischen Modell, das dem Alkoholkonsum die Rolle einer Ursache für einen Unfall zuweist.

Fazit

Um eine Ursache dingfest zu machen, benötigen wir einen regelhaften, dichten Zusammenhang. Den liefert uns ein Modell sehr wohl. Aber wir benötigen auch die Kenntnis der zeitlichen Reihenfolge und der konzeptuell-theoretischen Nähe der Ursache zur Wirkung. Diese können wir in einem Querschnittmodell nur selten wasserdicht belegen. Daher eignen sich Zeitreihenmodelle, die den zeitlichen Vorlauf einer Variablen mit in Rechnung besser, um Kausalität zu belegen.

Zeitreihenmodelle

An dieser Stelle ist vielleicht ein Ordnungsschema unterschiedlicher Modelle nützlich. Es findet sich in Abbildung 1.

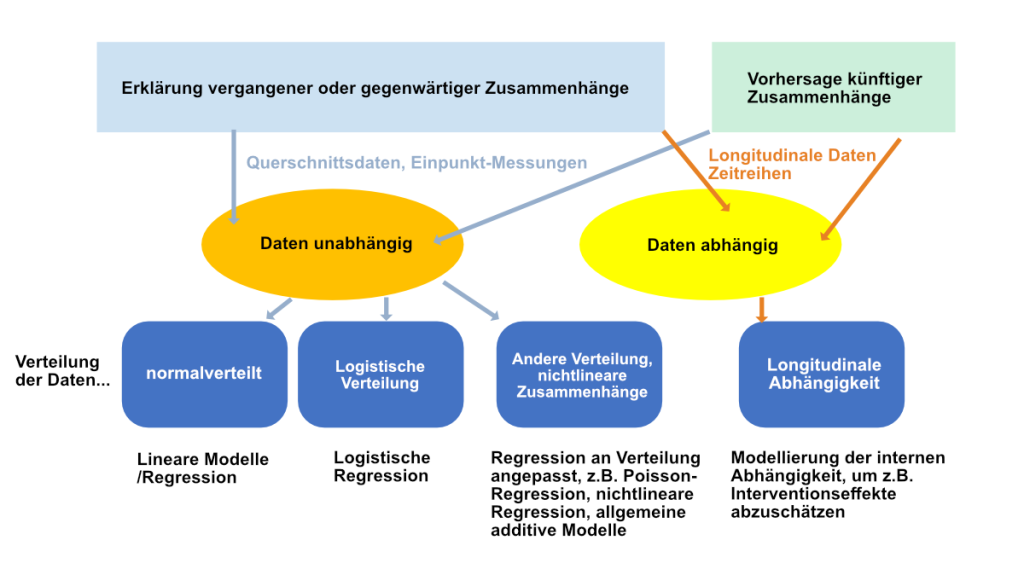
Man kann Modelle gliedern in solche, die sich mit der Erklärung bereits vorhandener Daten, etwa aus Vergangenheit und Gegenwart befassen und solche, die Voraussagen treffen wollen. Diese sind kategorial verschieden, denn sie machen notwendigerweise Annahmen über die Zukunft bzw. über die zu erwartende Datenstruktur, die mit empirischen Daten nicht belegbar sind.

Die Modelle, die wir oben besprochen haben, gehören der Kategorie der Erklärung vergangener oder gegenwärtiger Zusammenhänge an. Da in ihnen keine zeitlichen Komponenten vorkommen, ist es schwierig, Kausalitätsaussagen zu treffen. Man kann Kausalität bei diesen Modellen höchstens über theoretisches Verständnis gewinnen.

Unabhängige und abhängige Daten

Daten aus solchen Querschnittdatensätzen, etwa der unserer Covid-19-Mortalitätsmodellierung, sind immer Daten aus Einpunktmessungen, die statistisch voneinander unabhängig sind. Jede Einheit, z.B. jedes Land, stellt eine vom anderen Land statistisch unabhängige Einheit dar und ist technisch eine Zeile in einem Datensatz. Bei anderen Modellbildungen sind es oft auch einzelne Personen.

Sobald eine Einheit – ein Land, eine Schulklasse, eine Arztpraxis, ein Krankenhaus, eine Person – mehrmals gemessen und erfasst wird, sind diese Daten voneinander statistisch abhängig oder korreliert. Würden wir beispielsweise Covid-19 Todesfälle in Belgien in drei aufeinanderfolgenden Wochen erfassen und dasselbe in Deutschland machen, dann wären die Todesfälle je Land in je gleicher Weise von denen im anderen Land verschieden, weil sie miteinander korreliert sind. Man spricht von statistischer Abhängigkeit. Diese ist bei allen Zeitreihen gegeben, bei denen die gleiche Einheit – ein Land, eine Person – mehrfach über die Zeit gemessen wird.

Will man eine formale Kausalitätsanalyse mit Daten modellieren, so geht das nur über eine zeitliche Reihenfolge und damit über einen statistisch abhängigen Datensatz. Das symbolisiert der rote Pfeil oben, der vom langen blauen Block nach rechts ins gelbe Oval deutet. Man müsste also z.B. Datenreihen zu Fällen, Impfquoten, Vitamin-D-Status zu einem früheren Zeitpunkt haben und diese modellieren hinsichtlich ihrer Aufklärungskraft der Todesfälle zu einem späteren Zeitpunkt.

Diese Klasse von Modellen ist inhärent komplexer, weil man zuerst die statistische Abhängigkeit innerhalb der Reihen modellieren muss, bevor man die Zusammenhänge zwischen den Variablen klären kann.

Von links nach rechts signalisieren die blauen Blöcke immer komplexer werdende Verfahren. Der linke Block ist die im Methodenblog „Modellbildung und Regression“ besprochene lineare Regression. Der zweite Block ist das generalisierte lineare Modell, das wir zur Analyse der Covid-19-Mortalitätsdaten verwendet haben. Eine andere Subklasse dieser Modelle mit anderer Verteilung ist die logistische Regression, die die Aufklärung einer dichotomen Variablen leistet. Hier ist die Zielvariable ein dichotomes Merkmal, z.B. „krank“ oder „gesund“, „tot“ oder „lebendig“, „geimpft“ oder „nicht geimpft“ und die lineare Verkettung der Prädiktoren erfolgt als lineare Kombination von Prädiktoren als Exponentialfunktion von e, der Eulerschen Zahl. Das gleiche Prinzip wird angewandt, wenn die Verteilung der Kriteriumsvariable noch andere Formen, etwa eine Poissonverteilung, annimmt.

Wenn die Zusammenhänge schließlich nicht-linear werden, kommen nochmals andere Modelle zur Anwendung und die Schätzverfahren werden entsprechend anspruchsvoller. Mit modernen Computersystemen kann man schließlich verallgemeinerte additive Modelle rechnen, die grundsätzlich erst prüfen, ob nichtlineare Zusammenhänge vorliegen und diese dann modellieren.

Zeitreihen im eigentlichen Sinne

Um Kausalität abzuschätzen, sind Zeitreihenmodelle sehr nützlich, bei denen wir viele Datenpunkte zu einer Variablen haben, z.B. viele Messungen von Fällen und Todesfällen, oder von NPIs und Fällen, oder von Impfungen und Todesfällen.

Hier gilt es zuerst ein statistisches Modell zu finden, das die innere Abhängigkeit der Zeitreihen gut nachbildet. Dann kann man, z.B. über zeitverschobene Kreuzkorrelationen, prüfen, ob die eine Variable in ihrem Effekt der anderen vorausläuft bzw. die andere hinterherhinkt. Denn das ist die Voraussetzung für Kausalität: dass die Ursache vorausläuft. Würde beispielsweise die Impfung gegen SARS-CoV2 Todesfälle verhindern, dann würden wir erwarten, dass die Zeitreihe der Impfungen in einem Land der verringerten Mortalität in der Folge vorausgeht.

Dabei sind zwei Schritte zentral: Erstens die Struktur der inneren statistischen Abhängigkeit möglichst gut verstehen und modellieren; zweitens den zeitlichen Abstand zwischen vermuteter Ursache und erwarteter Wirkung optimal wählen. Bei der SARS-CoV2-Impfung etwa würden wir nicht erwarten, dass die Impfung sofort am nachfolgenden Tag zu weniger Covid-19 Todesfällen führt, sondern allenfalls nach 4 Wochen oder so.

Diese beiden Schritte sind komplex und machen solche Analysen fehleranfällig. Das gewählte Modell für die Modellierung der Zeitreihe ist zentral. Oft werden solche Modelle dann auch verwendet, um Voraussagen über die Zukunft zu machen. Viele Studien während der Coronakrise, die solche Prognosen abgaben und kolossal daneben lagen, waren solcher Art: Sie haben eine Modellannahme über die Struktur der Daten gemacht, manchmal auch ohne vorhandene Daten, und dann aufgrund dieser Modellannahmen Voraussagen errechnet.

Solche Modelle, das haben Spezialisten schon bald gesehen und kritisiert [4], sind extrem abhängig von den gemachten Annahmen über die Datenstruktur. Daher war z.B. das Imperial-College-Modell und das von ihm übernommene RKI-Modell zur Vorhersage dessen, was in der Pandemie unter welchen Umständen passieren wird, falsch [5, 6]. Ebenso waren die Abschätzungen der Wirkung der NPIs falsch [7, 8], und die Behauptung, dass der Lockdown in Deutschland Leben gerettet hat [9, 10]. In all diesen Fällen wurden Modellannahmen getroffen, bei denen schon leichte Verschiebungen um einige Tage oder ähnliche Änderungen sehr starke Auswirkungen haben und das Modell unpassend machen.

Meine eigenen Beispiele: ARIMA-Modelle zur Abschätzung der Effekte von Sferics auf Kopfschmerzen

Ich habe mich vor längerer Zeit intensiv mit solchen Zeitreihenmodellen und ihren statistischen Voraussetzungen befasst. Damals waren in der Psychologie und anderswo sogenannte ARIMA-Modelle en vogue. ARIMA ist das Akronym für eine Zeitreihen-Modellklasse und heißt „Autoregressive, integrated, moving average“ Modelle.

Dahinter verbirgt sich die Einsicht, dass Zeitreihen meistens autokorreliert sind, also der Wert, z.B. der Außentemperatur heute, mit dem von gestern, und möglicherweise auch von vorgestern, etc. korreliert ist. Dies ist die autoregressive Komponente der Zeitreihe. Man kann sie über eine Regressionsanalyse der Zeitreihe ermitteln, bei der man je einen, dann zwei, dann drei, usw. Werte der Vergangenheit verwendet, um den je aktuellen Wert abzuschätzen. Bleibt dann nur noch Rauschen übrig, also normalverteilte Residuen, dann hat man diese Komponente der Zeitreihe aufgeklärt. Dies ist also die autoregressive Komponente, als „A“ abgekürzt.

Schließlich sind Zeitreihen oft nicht stationär, das heißt, sie verändern ihr Niveau über die Zeit. Z.B. steigt die mittlere Temperatur übers Jahr an, oder die Covid-19-Todesfälle nehmen immer mehr zu. Solche Trends muss man korrigieren, indem man die Zeitreihe differenziert, d.h. man subtrahiert so lange Werte voneinander, bis die Zeitreihe stationär ist. Dies ist die integrierte Komponente, das „I“.

Und ganz zum Schluss haben Zeitreihen oft ein „Gedächtnis“, z.B. könnte es sein, dass das Wetter in wöchentlichen oder mehrtägigen Rhythmen schwankt. Dies drückt sich in der Korrelation der Residuen aus und ist der „moving average“, oder „MA“-Anteil der Zeitreihe.

Solche Zeitreihenanalyse, und analog auch andere, gehen nun so vor, dass sie diese statistischen Modellkomponenten der Zeitreihe abschätzen. Mit einer Residualdiagnostik lässt sich herausfinden, ob das Modell gut passt oder nicht. Dazu ist Fingerspitzengefühl und Erfahrung in hohem Ausmaß nötig.

Ich habe zweimal solche Analysen selber gemacht. Einmal mit einem Datensatz einer Langzeitbehandlung von Kopfschmerzen mit Homöopathie über ein ganzes Jahr, mit täglichen Tagebuchdaten [11, 12], und einmal mit Zeitreihen von Sferics-Messungen und Kopfschmerztagebuchdaten [13]. Ich kann daher ein Lied davon singen, wie zeitaufwändig, entscheidungsabhängig und fehleranfällig solche Analysen sind.

Der Trick dabei ist, dass man ein möglichst gutes statistisches Modell für die innere Abhängigkeit der Daten findet, sodass die Residuen zufällig streuen. Dann kann man z.B. eine zeitversetzte Korrelation, eine sog. Kreuzkorrelation zwischen zwei Reihen durchführen und erkennt dann, bei welchen Verschiebungen die Korrelationen wie hoch sind.

Wir haben in unserer Analyse von Kopfschmerz- und Sferics-Daten bei einem von 21 Patienten eine signifikante Kreuzkorrelation gefunden. Die Idee: Sferics sind ultrakurze und sehr schwache (nanoTesla) elektromagnetische Impulse in der Atmosphäre. Sie werden meistens von Wetterfronten erzeugt. Wir hatten damals die Möglichkeiten, Sferics-Daten von Prof. Betz von der TU-München zu verwenden. Kopfschmerzen, so sagen manche, könnten auch ein evolutionär frühes Warnsignal für heranrückende Wettergefahren dargestellt haben, sodass sensible Menschen, die sich rechtzeitig in Sicherheit brachten, einen Überlebensvorteil hatten. Man findet solche Zusammenhänge auch, aber eben nur bei etwa 5 % der Kopfschmerzpatienten, die wir untersucht haben.

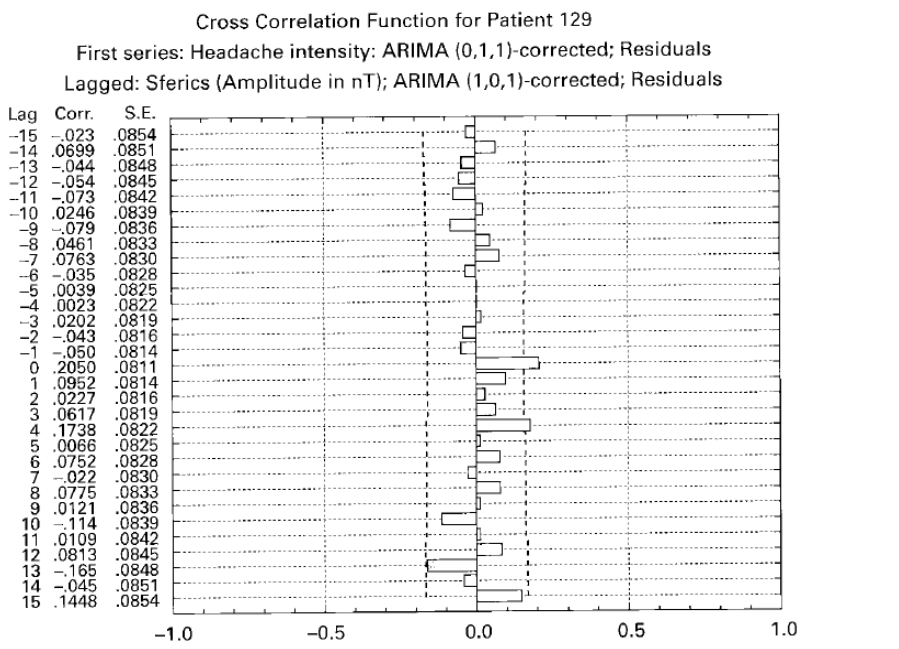
Abbildung 2 gibt die Originalabbildung unserer Publikation von 2001 wieder [13]. Die Zeitreihe der Kopfschmerzintensität, tägliche Daten von etwa einem Jahr, wurden mit einem ARIMA-Modell modelliert, das keine autoregressive Komponente, eine integrierte und eine Moving-Average Komponente hatte (daher: 0,1,1-Modell). Die Amplitude der Sferics Zeitreihe, auf Tage gemittelt, wurde ebenfalls statistisch modelliert mit einem (1,0,1)-Modell, also mit einer autoregressiven, keinem integrierten und einer Moving-Average-Komponente. Dann wurde die Sferics Zeitreihe verschoben („gelaggt“). Man erkennt: Es ergibt sich eine signifikante Kreuzkorrelation zum gleichen Zeitpunkt (lag 0) von r = .2. Nicht hoch, aber signifikant. Da die Sferics-Daten theoretisch potenzielle Ursachen sind und die Daten täglich gemittelt waren, haben wir das als ursächlichen Zusammenhang interpretiert. Bei 5 weiteren Fällen fanden wir Zusammenhänge, die aber unplausibel sind, weil die Zeitverschiebung negativ und zu groß war.

Das zeigt: oft sind solche statistischen Modelle nicht ausreichend gut in der Aufklärung der Datenstruktur und es kommt zu künstlichen, überblähten und unplausiblen Zusammenhangerfassungen.

Seither bin ich extrem vorsichtig, wenn es um die Abschätzung kausaler Zusammenhänge in Zeitreihen geht und äußert skeptisch, wenn andere davon berichten.

Das soll als Beispiel genügen, um das Prinzip einer kausalen Zeitreihenanalyse zu veranschaulichen.

Dies macht vielleicht auch plausibel, warum reine Augenscheindiagnostik bei Zeitreihen nicht klug ist. Denn Zeitreihen enthalten inhärente Dynamiken, die man erst kennen und verstehen muss, bevor man belastbare Aussagen zum Verlauf machen kann. Man kann allenfalls negative Aussagen treffen: wenn man klare Verläufe theoretisch erwartet hätte, dann sieht man an Zeitreihen auch ohne Analyse, ob dieser Verlauf eingetreten ist oder nicht. Aber umgekehrt herum positive Aussagen treffen ist schwierig.

Ich verwende zum Abschluss ein solches Beispiel. Abbildung 3 gibt Daten wieder, die ich der Webseite der Centers for Disease Control in den USA am 22.6.2022 entnommen habe. Es zeigt die sog. „all cause mortality“, also die Mortalität an allen Ursachen, von Altersschwäche bis Selbstmord, von Covid-19 bis „sudden death syndrome“, von Anfang 2018 bis Juni 2022. Die Daten sind unbereinigt und so, wie sie das CDC zur Verfügung stellt. Ich habe lediglich die Markerpfeile eingefügt, um bestimmte Zeitpunkte in etwa zu markieren.

Man erkennt zu Beginn des Jahres 2018 einen leichten Übersterblichkeitsgipfel. Der dürfte von der ausklingenden Grippesaison 2017/18 herrühren, die überall relativ stark war. Diese saisonale winterliche Sterblichkeitswelle erkennt man auch im Winter 2018/19, allerdings weniger stark ausgeprägt und ohne eine deutliche Übersterblichkeit, also eine Sterblichkeit, die über der statistischen Erwartung liegen würde.

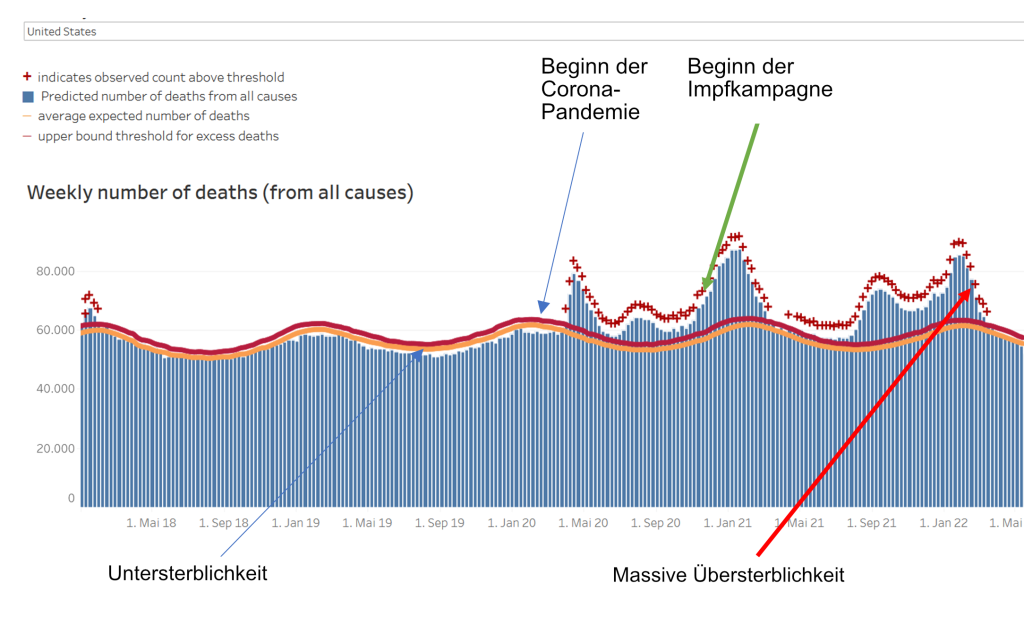
Diese statistische Erwartung ist durch die orange Kurve (Mittelwert) und die rote Kurve markiert (obere Vertrauensgrenze; aufgrund der Darstellung liegen diese Kurven nahe beieinander). Nach dem winterlichen Gipfel im Winter 2018/2019 folgt ein Untersterblichkeitstrog: im Sommer 2019 sterben weniger Menschen als üblich, weil die Anfälligen schon vorher gestorben sind. Dann Anfang 2020 beginnt die Corona-Welle 1 und danach die 2. Welle, untypischerweise im Sommer. Als die dritte Welle im Herbst 2021 beginnt, geht auch die Impfkampagne los, in den letzten beiden Wochen des Jahres 2021. Ob der dann folgende massive Anstieg der Übersterblichkeit damit zusammenhängt, dass die Coronawelle so massiv war, oder die Impfung in eine ansteigende Epidemiewelle (allem Lehrbuchwissen zum Trotz) diese Welle verschlimmert hat oder ob die Impfungen gar kausal für die steigenden Mortalitätsdaten waren, das lässt sich nicht sagen. Aber was man sieht ist: weder tritt die ansonsten übliche Untersterblichkeit auf, die sonst nach Epidemiewellen sichtbar werden, noch entspannt sich die Lage. Im Gegenteil: Die zwei Übersterblichkeitsgipfel im September 2021 und im Winter 2022 sind zusammengenommen massiver als der große davor.

Das Einzige, was man mit ziemlicher Sicherheit sagen kann: Die Covid-19 Impfungen habe nicht zu einer Senkung der Mortalität im Allgemeinen geführt und wenn, dann ist sie in diesen Daten nicht sichtbar.

Alles andere müsste man mit sorgfältigen Modellierungen der statistischen Abhängigkeiten und mit hypothetischen Interventionsmodellen testen. Wir wollen demnächst solche Modelle vorlegen.

Ich hoffe es ist klar geworden:

Zeitreihenanalysen sind komplex und von einer Vielfalt von Entscheidungen davon abhängig, welche Parameter wie gewählt werden und wie die Zeitreihe modelliert wird. Es gehört viel Zeit und Aufwand dazu. Man benötigt sehr viel Erfahrung. All das macht eine Zeitreihenanalyse anfällig für implizite Verzerrungen, z.B. aufgrund von Vormeinungen oder Erwartungen. Das ist in der Covid-19-Krise deutlich geworden. Denn hier wurden eine Vielzahl von Modellen publiziert, die sich anschließend als falsch herausstellten. Offenkundig wollten übereifrige Forscher Stütze für bestimmte Narrative liefern oder sind ihrer eigenen Vormeinung aufgesessen. Forscher sind schließlich auch nur Menschen.

Quellen und Literatur

1. Hume D. A Treatise of Human Nature. London: Dent; 1977 1977/ / /1911.
2. Goddu A. William of Ockham’s arguments for action at a distance. Franciscan Studies. 1984;44:227-44.
3. Ockham Wv. Expositio in libris Physicorum Aristotelis. In: Etzkorn GI, editor. Opera Philosophica. 5. St. Bonventure: Franciscan Institute; 1957. p. 616-39.
4. Daunizeau J, Moran RJ, Mattout J, Friston K. On the reliability of model-based predictions in the context of the current COVID epidemic event: impact of outbreak peak phase and data paucity. medRxiv. 2020:2020.04.24.20078485. doi: https://doi.org/10.1101/2020.04.24.20078485.
5. Ferguson N, Laydon D, Nedjati Gilani G, Imai N, Ainslie K, Baguelin M, et al. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. London: Imperial College, 2020.
6. an der Heiden M, Buchholz U. Modellierung von Beispielszenarien der SARS-CoV-2-Epidemie 2020 in Deutschland. Berlin: Robert Koch Institut, 2020.
7. Chin V, Ioannidis JPA, Tanner MA, Cripps S. Effect Estimates of COVID-19 Non-Pharmaceutical Interventions are Non-Robust and Highly Model-Dependent. Journal of Clinical Epidemiology. 2021. doi: https://doi.org/10.1016/j.jclinepi.2021.03.014.
8. Flaxman S, Mishra S, Gandy A, Unwin HJT, Mellan TA, Coupland H, et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020. doi: https://doi.org/10.1038/s41586-020-2405-7.
9. Dehning J, Zierenberg J, Spitzner FP, Wibral M, Neto JP, Wilczek M, et al. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science. 2020;369(6500):eabb9789. doi: https://doi.org/10.1126/science.abb9789.
10. Kuhbandner C, Homburg S, Walach H, Hockertz S. Was Germany’s Lockdown in Spring 2020 Necessary? How bad data quality can turn a simulation into a dissimulation that shapes the future. Futures. 2022;135:102879. doi: https://doi.org/10.1016/j.futures.2021.102879.
11. Walach H, Lowes T, Mussbach D, Schamell U, Springer W, Stritzl G, et al. The long-term effects of homeopathic treatment of chronic headaches: One year follow-up. Cephalalgia. 2000;20:835-7.
12. Walach H, Lowes T, Mussbach D, Schamell U, Springer W, Stritzl G, et al. The long-term effects of homeopathic treatment of chronic headaches: one year follow-up and single case time series. British Homeopathic Journal. 2001;90:63-72.
13. Walach H, Betz H-D, Schweickhardt A. Sferics and headache: a prospective study. Cephalalgia. 2001;21:685-90.