Einige grundlegende Überlegungen zur Methodik der Meta-Analyse und zu ihren Grenzen und Möglichkeiten
Wir kennen alle diese Momentaufnahmen von Menschen in Bewegung. Je heftiger die Bewegung, desto schräger sind oft die Aufnahmen – Fußballer mit wutverzerrtem Gesicht, Pferde im Sprung mit vor Angst geweiteten Augen, Frauen, die grad was Schlimmes sehen und Entsetzen im Gesicht ausdrücken, unsere Liebsten, wie sie gerade irgendeinen Lieblingsbissen in den Mund stecken, dabei die Augen zuhaben und so dreinschauen, als könnten sie nicht auf drei zählen. Und wir wissen alle, dass solche Momentaufnahmen nur wenig über die Dynamik aussagen, die zu diesem Bild geführt haben und von dem Bild wieder wegführen, und nur in Ausnahmefällen sagen sie etwas über des Wesen des Abgebildeten aus.
So ähnlich ist es auch mit Meta-Analysen: Sie sind Momentaufnahmen in einem dynamischen Prozess. Im Ideal der Theorie fassen sie verschiedene Studien zusammen und destillieren eine „wahre“ Effektgröße heraus, die im Rauschen der einzelnen Studien, in ihrer mangelnden statistischen Mächtigkeit oder in zufälligen Schwankungen verborgen sind. Aber dieses Ideal geht immer davon aus, dass es so etwas wie eine „objektiv wahre Größe“ wirklich gibt. Eine Untersuchung der Frage, ob diese Annahme vernünftig ist, heben wir uns für spätere Überlegungen auf. In der Praxis ist es jedoch eher so: Es gibt Serien von Studien, manche positiv, manche negativ, manche unentschieden und je nachdem, welche man gerade zur Hand hat, oder welcher man den Vorzug gibt, entscheidet man sich für dieses oder jenes Ergebnis.
Da helfen Meta-Analysen, um die gerade und bis jetzt vorliegenden Ergebnisse zu verdichten. Was aber, wenn eine neue Studie kommt? Es könnte immerhin sein, dass eine neue Studie ganz andere, neue oder völlig gegensätzliche Ergebnisse zu Tage fördert. Das ist in der Forschung nicht selten so. Plötzlich taucht eine neue Betrachtungsweise auf und die Ergebnisse einer Meta-Analyse bröckeln. Meta-Analysen von Anti-Diabetika-Studien z.B. zeigen, dass sie eine beträchtliche Effektstärke aufweisen, um den Blutzucker in Grenzen zu halten. Aber dummerweise steigern sie die Mortalität, etwas, das sie ursprünglich eigentlich hätten verhüten sollen. Das ist nur ein Beispiel.
[raw]
Die Meta-Analyse beantwortet im wesentlichen zwei Fragen:
1. Ist tatsächlich, über die untersuchten Studien hinweg, ein statistisch signifikanter Effekt vorhanden?
2. Wie groß ist der Effekt über alle Studien hinweg.
Die Interpretation überlässt sie, wie oft in der Forschung, dem Forscher bzw. den Lesern der Analyse.
[/raw]
[raw]
[/raw]
Gerade eben ist eine neue Meta-Analyse erschienen, die versucht die Frage zu beantworten: wirken individualisierte homöopathische Arzneimittel besser als Placebo [1]. Sie sammelte alle Studien, die in irgendeiner Form homöopathische Arzneimittel individualisiert einsetzten, insgesamt 32, schloß diejenigen aus, die nicht analysierbar waren und kam zu einem positiven Ergebnis: Individualisierte Homöopathie, so das Ergebnis, lässt sich von Placebo unterscheiden.
Die sog. Odds Ratio betrug 1.53 für alle Studien und 1.98 für die drei Studien mit den zuverlässigsten Daten. Eine „Odds Ratio“ ist ein Effektstärke-Maß, das binäre, also dichotome Daten, ins Verhältnis setzt. Es ist das Verhältnis von Gebesserten zu Verschlechterten oder nicht Gebesserten in der einen Gruppe im Verhältnis zur Zahl der Gebesserten im Verhältnis zu den Verschlechterten in der anderen Gruppe. Wenn diese Verhältnisse in jeder Gruppe gleich sind, ist die Odds-Ratio 1.0.
Das leuchtet sofort ein: wenn in einer Gruppe 20% gebessert sind und in der anderen Gruppe auch, dann ist das Verhältnis oder die „ratio“ von 20/20 gleich 1. Arithmetisch wäre das also 20/100 : 20/100. So ist die Odds-Ratio definiert. Nun kann man sich daran leicht klar machen, dass diese Maßzahl insofern praktisch ist, als sie unabhängig davon ist, wie groß die jeweiligen Zahlen in den Gruppen waren; denn 2/10 : 20/100 würde genauso 1.0 ergeben wie 2/10 : 200/1000.
Was auch praktisch ist, ist die Tatsache, dass diese Zahlen unabhängig davon sind, wie genau die Ergebnisse bestimmt wurden. Es könnte z.B. ein Verhältnis von 20 Kranken zu 100 Gebesserten sein, oder 20 Toten zu 100 Lebendigen, oder 20 Leute deren Intelligenzquotient größer als 130 ist zu 100, deren Intelligenzquotient darunter liegt, oder sonst irgendwie festgestellte Kriterien.
Auch das ist schön an Meta-Analysen: sie überführen individuelle Studienergebnisse in unabhängige, abstrakte Metrik. Die oben genannten Zahlen einer Odds-Ratio von 1.53 bzw. 1.98 kann man so interpretieren: eine Person der Behandlungsgruppe – in diesem Falle „individualisierte Homöopathie“ – hat eine 53% höhere Chance mit den vorgelegten Kriterien als gebessert zu gelten als in der Placebo-Gruppe bzw. eine 98% höhere Chance. Man kann mit einer Meta-Analyse auch die statistische Signifikanz der gefundenen gemeinsamen Zahl ermitteln.
Das funktioniert wie bei anderen Signifikanz-Tests auch: man errechnet den sog. Standardfehler und ermittelt mit dessen Hilfe den Bereich, innerhalb dessen 95% aller Werte liegen (siehe mein Blog über Statistik). Wenn dieser sogenannte Konfidenzbereich den Wert 1.0, also den Wert, an dem kein Effekt vorhanden ist, ausschließt, dann ist die gefundene mittlere Kenngröße, in diesem Fall die Odds-Ratio von 1.53, „signifikant“, liegt also mit 95%iger Wahrscheinlichkeit innerhalb eines Bereiches, der den Null-Effekt ausschließt. Das ist hier in der Tat der Fall.
Insofern sind die Forscher auch berechtigt zu sagen, individualisierte Homöopathie unterscheidet sich offenbar von Placebo. Und zwar in den Studien, die individualisierte Homöopathie untersuchten. Und zwar nur in denen, die hier zusammengefasst wurden. Sobald eine oder zwei, oder gar drei Studien vorliegen, die einen drastisch anderen Wert haben, kann sich diese Zusammenfassung wieder verschieben. Denken wir an die Fotographien von sich bewegenden Menschen oder Tieren.
Der Geltungsbereich der Analyse hängt also sehr stark von den eingeschlossenen Studien ab. Die Autoren haben insofern sehr sauber gearbeitet, als sie – dies eine Voraussetzung – vorher genau definiert haben, welche Studien sie einschließen und ausschließen wollen. Denn würde man das hinterher tun, könnte man ja die Ergebnisse zusammenbasteln.
Was das genau heißt, will ich kurz an zwei Beispielen demonstrieren. Meine eigene Studie zu klassisch-homöopathischer Therapie von chronischen Kopfschmerzen gehört aus meiner Sicht immer noch – das sage ich durchaus unbescheiden – zu den methodisch aufwändigsten klinischen Studien, die klassische Homöopathie untersucht haben [2]. Dummerweise gehört sie auch zu den Studien, mit den größten negativen Effektstärken (etwa d = -0.5; ich werde gleich noch was zu diesem Maß sagen). Das heißt, ihr Effekt zeigt in die „falsche“ Richtung, weil in dieser Studie die Placebo-Gruppe tendenziell sogar besser war. Diese Studie war nun in der hier vorliegenden Meta-Analyse nicht eingeschlossen. Warum nicht? Habe ich mich und die Autoren gefragt. Ganz einfach, war die Antwort: wir haben keine Mittelwerte und Standard-Abweichungen berichtet, sondern robuste Werte wie Median und Perzentile, und wir haben auch keine Statistik berichtet (weil die Werte in eine von der Hypothese aus gesehen falsche Richtung gegangen sind und daher kein Test sinnvoll und notwendig war). Daher waren die Autoren auch berechtigt, sie auszuschließen, richtig und laut meta-analytischer Logik lege artis. Aber was wäre gewesen wenn diese – oder gar noch mehr – negative Studien in die Rechnung eingeflossen wären? Möglicherweise wäre der Effekt plötzlich verschwunden. So schnell kann es gehen. Denn Meta-Analysen sind ein Schnappschuss im Strom der Erkenntnis.
Ein anderes Beispiel ist die vorausgegangen Meta-Analyse von Shang et al [3]. Im Unterschied zur Analyse von Mathie und Kollegen, die wir hier besprechen, wurden von Shang et al. keine inhaltlichen oder formalen Kriterien angelegt. Vielmehr beschlossen diese Autoren aus Gründen, die sie nie deutlich gemacht hatten, nur einen Teil der Studien, nämlich insgesamt 8 der über 120 Studien, die in ihrer Sammlung waren, für die Meta-Analyse heranzuziehen. Offiziell gaben sie als Grund an: die grössten Studien.
Naja, kann man vertreten. Aber warum haben sie dann ausgerechnet meine Studie [2] noch dazu genommen. Wenn man irgendwelche formalen Kriterien für „Grösse“ nimmt, dann könnte man sagen: alles was grösser als 100 oder 200 Patienten ist. Dumm, dann hätten sie meine weglassen müssen; die hatte nämlich nur 98 Patienten. Ich habe mich nie des Eindrucks erwehren können, dass diese Auswahl eine willkürliche war: denn mit meiner Studie blieb die Analyse unterhalb der Signifikanz-Grenze. Ordnet man alle Studien der Grösse und nimmt man mehr Studien hinzu, dann wird die Analyse plötzlich signifikant. Das haben damals Lüdtke und Rutten [4] in einer sorgfältigen Re-Analyse sehr deutlich zeigen können.
Das heißt: Ob man mithilfe einer Meta-Analyse zum Schluss kommt, ob Homöopathie sich von Placebo unterscheiden lässt oder nicht, hängt im Wesentlichen davon ab, welche Studien man in die Auswahl nimmt und welche man weglässt. Damit will ich Mathie und Kollegen keineswegs unterstellen, sie hätten manipuliert. Sie haben sich, das hat mir Robert Mathie auch in einer Korrespondenz nochmals versichert, strikt an ihr Protokoll gehalten. Da ich ihn gut kenne, habe ich keinen Zweifel an der Richtigkeit dieser Aussage. Aus meiner Sicht haben die Autoren Glück gehabt. Lassen wir es ein paar mehr oder andere Studien sein, die Situation könnte sich leicht ändern.
Das sieht man schon daran, dass die Vorgänger-Meta-Analysen zu völlig konträren Ansichten kommen, obwohl sie im Wesentlichen die gleiche Datengrundlage zur Verfügung haben: ausser Shang [3] wären da noch zu nennen Cucherat und Kollegen [5] und Linde und andere [6]. Woher kommt das? Linde und Kollegen beschlossen, möglichst alle Daten zu verwenden. Das ist eigentlich der normale Standard. Und dabei fanden sie einen robusten, statistisch signifikanten Effekt.
Cucherat und andere verwendeten zwar auch alle Daten und erhielten ein signifikantes Ergebnis. Dann verwendeten sie aber nur die Studien, die sie als „die besten“ ansahen und die Signifikanz schmolz dahin. Was nun aber „die besten“ Studien sind ist immer auch ein Stück Ansichtssache. (siehe Box „Studiengüte und Meta-Analyse“ weiter unten) Deshalb haben ja Mathie und Co. in dieser neuen Analyse ein striktes Protokoll angewandt und vorher definiert, wie sie vorgehen wollen. Und, was wichtig ist, sie haben die zu untersuchende Intervention genau beschrieben: nämlich klassische individualisierte Homöopathie. Also wurden nur solche Therapie-Studien eingeschlossen, die die Homöopathie nach Hahnemann angewandt untersuchten. Das ist folgerichtig.
Denn wenn man die sogenannte „Modell-Validität“ nicht berücksichtigt, also die Frage, ob auch wirklich das in einer Studie abgebildet wurde, was in Wirklichkeit passiert oder idealerweise passieren soll, dann untersucht man ja logischer Weise eine Chimäre. Viele Homöopathie-Studien haben diese sub-optimal operationalisiert, also die Frage „Was genau verstehen wir unter Homöopathie?“ schlecht beantwortet und umgesetzt. Das hat diese neue Meta-Analyse nun vermieden, indem nur „klassisch homöopathische individualisierte Therapie“ untersucht wurde.
Das Bild, das sich präsentiert ist, wie gesagt, positiv. Ob es so bleiben wird, wird im wesentlichen davon abhängen, ob weitere Studien hinzukommen, die dieses Bild bestätigen. Ich persönlich bin da aus theoretischen Gründen eher skeptisch, lasse mich aber gerne überraschen. Das ist im übrigen auch der Grund, weswegen die Cochrane Collaboration ihre Reviews und Meta-Analysen in regelmäßigen Abständen immer wieder auf den neuesten Stand bringt. Denn wenn eine neue Studie kommt, ändert sich die Lage, manchmal sogar drastisch. Das hat sich etwa bei der Analyse zu Tamiflu und den Neuraominidase-Hemmern gezeigt und kann sich hier bei der Homöopathie wiederholen.
[raw]
Dieser Gedanke ist nicht ganz von der Hand zu weisen und steht etwa hinter den Überlegungen zur Einschränkung der Datenbasis bei Cucherat [5]. Dem gegenüber steht die Meinung, dass sich über die Menge der synthetisierten Studie eben auch das Rauschen ausmittelt, das von den Schwankungen methodisch schlechter Studien kommt, die daher möglichst alles einschließen wollen. Das haben etwa die Autoren der historisch gesehen einflussreichsten Meta-Analyse zur Wirksamkeit der Psychotherapie (die damals Eysencks Invektive ausgelöst hatte), Smith & Glass so gemacht [14]. Vor allem wenn man am Anfang einer Forschungsentwicklung steht, ist eine solche Vorgehensweise sinnvoll. Man kann dann in einer sog. „Sensitivitätsanalyse“ prüfen, was passiert, wenn man etwa Studien mit einem bestimmten Design oder anderen Merkmalen ein- und ausschließt und die Analyse wiederholen. Ein solches eher exploratorisches Vorgehen gibt dann sehr oft wertvolle Hinweise darauf, welche Faktoren die Effektgröße beeinflussen, sog. moderierende Variablen.
Manche Autoren entscheiden sich dafür, nur die methodisch stringentesten Studien in eine Meta-Analyse einzubeziehen und schließen alle Studien aus, die z.B. nicht randomisiert sind, oder nicht gegen eine aktive oder Placebo-Kontrolle durchgeführt wurden. Das wurde auch in der hier vorliegenden Analyse von Mathie und Kollegen so gemacht. Aufwändige Meta-Analysen kodieren die Studiengüte mit einem sehr komplexen Kodierschema, das natürlich vorher festgelegt sein muss. Man kann dann, wenn man das möchte, die Studiengüte in einem numerischen Wert ausdrücken, den man etwa zur Gewichtung der Studien verwendet. Dann würden nur die Studien, die wirklich sehr gut sind zu 100% in die Analyse eingehen und die anderen mit entsprechend weniger Gewicht. Das haben Ende der 80er Jahre Wittmann und Matt getan und damit durchaus zeigen können, dass sorgfältige Studien starke Effektgrössen von Psychotherapie dokumentieren, wohingegen methodisch schludrige die Psychotherapie eher schlechter wegkommen ließen [15].
Das Cochrane Handbuch und verschiedene neuere Analysen wählen einen Mittelweg: Sie schlagen vor, die einzelnen Studien nach ihrem „risk of bias“ einzuschätzen, also danach, wie groß das Risiko ist, dass man sich täuscht. Im Prinzip ist das eine grobe Bewertung der internen Validität einer Studie. Es werden die wichtigsten Kriterien dokumentiert: ob eine Studie randomisiert war oder nicht, ob die Zuweisung zu den Gruppen verblindet war, ob die Teilnehmer und die Untersucher verblindet waren, ob es eine hohe Drop-Out Rate gab (das gibt in etwa Auskunft über die Güte der Organisation einer Studie und die Akzeptanz der Intervention). Manchmal wird auch noch dokumentiert, ob Zielkriterien apriori festgelegt waren. Man kann dann diese Einschätzungen deskriptiv nutzen, oder man kann sie nutzen, um mit Untergruppen von Studien Teilnanalysen zu rechnen, die Auskunft darüber geben, ob etwa methodisch weniger stringente Studien zu einer Überschätzung des Effektes neigen und also ob methodische Güte eine Rolle spielt oder nicht. Manchmal tut sie es, manchmal nicht. Man muß auch genau hinsehen: nicht immer bekommen die Autoren diese Ratings sauber hin. Oft werden Hilfskräfte eingesetzt, die sich zu wenig auskennen; oder eine Studie berichtet vielleicht nicht sorgfältig genug, etwa weil sie nur als „Research Letter“ mit wenig Platz publiziert wurde. In einem solchen Falle wäre es nötig, bei den Autoren die Informationen einzuholen.
Methodische Studiengüte als eine Variable quantitativ, also im Sinne einer Gewichtung, zu verarbeiten, ist sehr aufwändig. Daher machen es wohl auch die wenigsten Autoren. Denn viele Studiendetails kann man aus publizierten Berichten nicht entnehmen, sondern müsste sie bei Autoren erfragen. Das geht meist nur bei kürzlich publizierten Studien.
Diese Argumentation und diese Argumente werden von manchen Autoren auch dazu genutzt, die Komplexität zu reduzieren und relativ strikte Ein- und Ausschlußkriterien anzuwenden. Damit erleichtern sie sich das Leben, weil weniger Material zu bearbeiten ist. Ob sie damit der Sache einen Dienst tun, ist eine ganz andere Frage. Ich persönlich finde die Einschränkung von Meta-Analysen nur auf randomisierte Studien nicht sinnvoll. Denn damit nimmt man sich die Möglichkeit exploratisch zu untersuchen, welche Variablen zur Variation des Effektes beitragen (siehe unten: Box Homogenität und Moderatoranalyse)
[/raw]
Noch einen anderen Punkt wollte ich ansprechen: Mathie und Kollegen verwendeten die Odds-Ratio als Kennzahl. Dies ist wie gesagt eine Effektstärke, die sich auf dichotome Maße und Variablen bezieht. Solche Variablen kommen in der Natur vor, werden aber eher von uns durch Reduktion von Information erzeugt. Sie kommen natürlicherweise vor, wenn wir etwa Eigenschaften wie „tot“ und „lebendig“ betrachten. Die sind klarerweise dichotom. Aber die meisten anderen Eigenschaften und Variablen sind eigentlich natürlicherweise kontinuierlich: Gesundheit und Krankheit etwa sind in der Regel eher auf einem kontinuierlichen Spektrum angeordnet, genauso wie Wohlbefinden, Energie, Lebensqualität, Stärke von Symptomen, gefühlte innere Zufriedenheit, Blutdruckwerte, immunologische Kennwerte, Intelligenz, usw. Erst unsere Tendenz Information zu reduzieren macht dann daraus so etwas wie: „gesund“ vs. „krank“, „hat eine Diagnose“ oder „hat keine Diagnose“, „ hat einen Rückfall“ oder „hat keinen Rückfall“, „ist gescheit“ oder „ist dumm“, „ist glücklich“ und „nicht depressiv“ oder „unglücklich“ und „depressiv“.
Wir sehen: In der Regel ist die Verwendung eines dichotomen Maßes und damit der Odds Ratio als Kennzahl einer Informationsreduktion geschuldet und kommt natürlicherweise nur dort vor, wo Mortalität oder das Vorkommen einer Serie von Ereignissen – Krankenhauseinweisung, Operation oder Reha nötig – dichotom gewertet wird. Mediziner machen das gerne, weil sie denken, dadurch erhöht sich die klinische Relevanz. Denn in der Klinik müssen schließlich Entscheidungen getroffen werden, die auch dichotom sind: Operieren wir oder nicht? Geben wir eine Medikation oder Intervention oder nicht? Muss der Mensch klinisch überwacht werden oder darf er nach Hause? Und so sind einige der in dieser Meta-Analyse zusammengefassten Studien implizit auf solchen dichotomen Ergebnis-Massen aufgebaut.
In sehr vielen Fällen aber verwenden wir kontinuierliche Maße. Das ist wiederum eine Frage der akademischen Kultur. Psychologen etwa versuchen, möglichst kontinuierliche Maße zu konstruieren, etwa indem sie viele einzelne Fragen, sog. „Items“, kombinieren, um einen kontinuierlichen Wert auf einer Skala zu erzeugen. Das geschieht etwa bei klassischen Tests wie Intelligenztests, oder bei Persönlichkeitsfragebögen. Aber auch bei sog. klinischen „Outcome-Maßen“, die klinische Veränderungen messen sollen, etwa Depressionsfragebögen, Fragebögen zur Lebensqualität, Schmerzskalen, Symptomenscores, wo immer möglich versuchen wir die Kontinuität des Geschehens, das bei uns Menschen abläuft, abzubilden in kontinuierlichen Maßen.
Dann berichten Studien z.B. über unterschiedliche Werte in einem Maß der Lebensqualität zwischen zwei Gruppen, oder über verschiedene mittlere Schmerzwerte, oder Anzahl der Tage, an denen ein Symptom aufgetreten ist, usw. In solchen Fällen haben wir es dann mit kontinuierlichen Maßen zu tun. Diese werden in aller Regel berichtet als mittlere Werte, die in einer Gruppe gefunden werden und die Werte in dieser Gruppe zusammenfassend beschreiben, und der Streuung dieser Werte in einer Gruppe. Manchmal nimmt man auch robuste Masse, wie den Median, der den Punkt beschreibt, oberhalb dessen 50% aller gemessenen Werte liegen. Bei regelmäßiger Verteilung sind sich Mittelwert und Median in der Regel sehr nahe. Nur wenn es große Ausreißer gibt, über- oder unterschätzt der Mittelwert und dann nimmt man lieber den Median.
Solche Studien fasst man in einer Meta-Analyse zusammen über das Effektstärke-Maß „d“ (für „Differenz“), das manchmal auch als „SDM“ („standardized mean difference – standardisierter mittlerer Unterschied“) bezeichnet wird oder in einer bestimmten Form als „g“, wenn „d“ durch einen Faktor reduziert wurde, der die unterschiedliche Studiengröße mit berücksichtigt. Ich habe in meinem Blog über „Power“ („Die Magie der Statistik“) etwas ausführlicher darüber geschrieben und wiederhole hier nur noch kurz:
„d“ kommt zustande, indem man die Mittelwerte der beiden Gruppen voneinander subtrahiert, also eine Differenz zwischen den Gruppen bildet. Diese zeigt die Größe des Unterschieds zwischen den Gruppen an. Wenn man es jetzt nur mit Werten der gleichen Kategorie zu tun hätte, z.B. nur Blutdruckwerten, oder nur mit Intelligenz-Werten, oder nur mit Werten einer bestimmten Depressionsskala, dann könnte man es dabei belassen, denn man hat einen Unterschied quantifiziert. Aber weil wir ja oft ganz unterschiedliche Dimensionen vor uns haben, müssen wir uns einen Trick einfallen lassen, um die Differenzen vergleichbar zu machen. Das geschieht z.B. bei der Odds Ratio, indem man nicht nur die gebesserten Patienten in jeder Gruppe betrachtet, sondern die Gebesserten im Verhältnis zu allen Patienten.
Bei den kontinuierlichen Maßen gelingt einem dieser Trick der Vergleichbarmachung durch die sog. „Standardisierung“ (daher auch SDM): man dividiert die Differenz durch die Standard-Abweichung, also die Streuung der Werte in einer Gruppe. Die Streuung ist definiert durch die Abweichung der einzelnen Werte vom Mittelwert [7]. Um also die Differenzen vergleichbar zu machen, werden sie durch die Standard-Abweichung dividiert und somit standardisiert. Das bedeutet: man kann die Differenzen aus, sagen wir Unterschieden gemessen in Millimetern Quecksilbersäule, vergleichen mit Differenzen, gemessen mit einem Intelligenztest oder mit Differenzen gemessen mit einer Lebensqualitätsskala. Der Unterschied ist eine dimensionslose Zahl „d“, die man allenfalls als multiple Zahl einer Standard-Abweichung interpretieren kann. Meine oben genannte negative Effektgröße meiner eigenen Studie d= -0.5 betrug also etwa eine halbe Standard-Abweichung Verschlechterung für die behandelte Gruppe.
Ich persönlich finde Meta-Analysen, die auf der Effektstärke d beruhen, etwas aussagekräftiger. Aber im wesentlichen hängt das davon ab, welche Maße in den originalen und zusammengefassten Studien mehrheitlich verwendet wurden. Viele Meta-Analysten gehen nun so vor, dass sie nur solche Studien in ihre Analyse einbeziehen, die das von ihnen favorisierte Maß zur Berechnung verwenden oder erlauben und ignorieren die anderen. Das ist schlechte Praxis. Manche Analysen führen dann schon eher zwei getrennte Analysen durch, für jede Metrik eine. Das ist schade, weil dadurch genau die Stärke der Meta-Analyse verloren geht, nämlich die statistische Power der einzelnen Studien zu bündeln und dadurch zu einer kompakteren Aussage zu kommen. Die meta-analytischen Spezialisten transformieren in der Regel die Metriken ineinander. Hierzu gibt es verschiedene Möglichkeiten. Man kann z.B. Odds Ratios und ähnliche Masse über eine Arcsinus-Transformation in einen Wert überführen, den man als d-Wert interpretieren kann. Oder man kann eine Formel anwenden, die Hasselbald & Hedges vorgestellt haben [8], mit der man in die eine und in die andere Richtung transformieren kann, also d-Werte in Odds-Ratios überführen und umgekehrt. Das hat meines Wissens die Analyse von Linde [6] getan. Die hier vorliegende Analyse hat ein einfacheres, später publiziertes Verfahren verwendet, das aber auch von der Cochrane Collaboration verwendet wird und im wesentlichen gute Schätzungen liefert [9]. Hier wurde die Transformation von kontinuierlichen Werten, also d zur Odds-Ratio vorgenommen, ungeschickt ist, weil ja die meisten Studien in der Tat kontinuierliche Zielgrößen hatten und dadurch Information verloren geht.
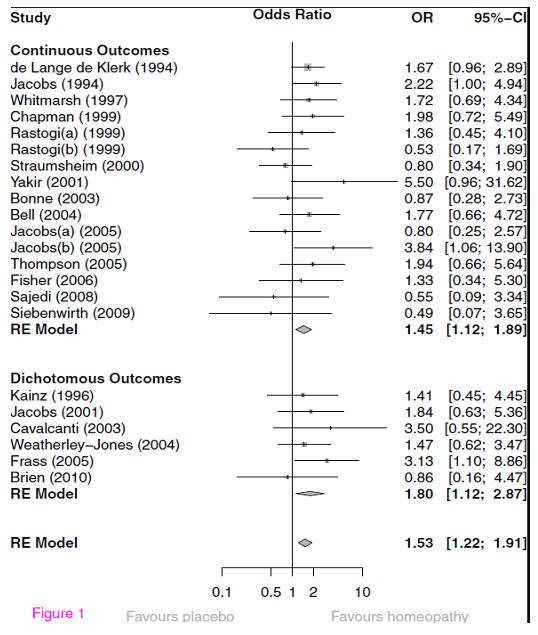
Ich bilde hier unten die Originalgrafik der zusammenfassenden Analyse ab:
Abb. – Sog. „Forest Plot“ der einzelnen Effektgrössen und der gemittelten Effektstärke: Odds Ratio individualisierte Homöopathie vs. Placebo.
Diese Abbildung ist Standard in Meta-Analysen. Wir verwenden ein bisschen Aufmerksamkeit auf ihre Interpretation. Zunächst sehen wir, dass die meisten Studien kontinuierliche Zielgrößen verwendet haben; sie wurden aber mittels der oben besprochenen Transformation in Odds Ratios verwandelt. In der unteren Sektion sind dann die Studien, die in der Tat dichotome Outcomes berichten und die auch richtiger Weise mit Odds Ratios abgebildet werden. Hier hätte man sich durchaus ein umgekehrtes Vorgehen vorstellen können. Links sind die einzelnen Studien benannt, jede Zeile bildet eine Studie und die Zahl unter der Überschrift „OR“ gibt die „odds ratio“ an. In der Grafik dazwischen ist die gleiche Zahl und das zugehörige Konfidenzintervall graphisch als Punkt unterschiedlicher Größe abgebildet. Das 95%ige Konfidenzintervall, das in eckigen Klammern neben der OR numerisch und in der Graphik als Strich aufgeführt ist, zeigt, wie sicher die Schätzung der OR ist und gibt die individuelle Signifikanz der Studie an.
[raw]
Anders ausgedrückt: Variable (was gemessen wird) und Parameter (was dem Gemessenen zugrunde liegt) sind dann identisch. Praktisch gesehen wird man aber nie alle Werte erfassen können und wollen. Das ist ja der Trick bei der Statistik, dass man sich Totalerhebungen nach Möglichkeit spart. Diesen Trick bezahlt man mit einer Unsicherheit der Schätzung. Es ist unmittelbar einleuchtend, dass die Präzision der Schätzung in direktem Zusammenhang steht mit der Größe der gezogenen Stichprobe (und ihrer Repräsentativität). Wenn wir etwa bei allen Personen einer Stadt den Blutdruck messen, dann hat unsere Messung keine Unsicherheit und der mittlere Blutdruck, den wir gemessen haben ist identisch mit dem mittleren Blutdruck der Bevölkerung in der Stadt. Wenn wir das nur bei jedem 10. Bewohner tun, dann schätzen wir den mittleren Blutdruck der Bevölkerung aufgrund unserer Daten und haben natürlich mit einer Unsicherheit zu rechnen.
Mathematisch drückt sich das so aus, dass wiederum standardisiert wird und zwar in diesem Falle durch die Wurzel der Gesamtzahl unserer Messungen. Das bedeutet: je mehr Werte wir haben, desto geringer wird unsere Schätzunsicherheit. Diese Tatsache macht sich das Konfidenzintervall zu Nutze. Denn der Standardfehler der Schätzung, so heißt er, kann wiederum so interpretiert werden, dass er einer Standardnormalverteilung folgt, bei der der Standardfehler die Standard-Abweichung dieser Verteilung repräsentiert. Weil die Gesamtfläche der Verteilung genormt ist und „1“ ergibt, kann man die Fläche unter der Kurve als Wahrscheinlichkeit interpretieren. Also kann man mit Hilfe dieses Standardfehlers ausrechnen, unter welchem Flächenabschnitt 95% aller Werte zu liegen kommen werden. Dies sind immer 1.96 * Standardfehler (der in diesem Falle die Standard-Abweichung dieser Verteilung darstellt) aller Werte links und rechts des Mittelwertes dieser Verteilung, weil die Fläche, die links der Ordinatenpunkte von + oder – 1.96 zusammen 5% der Fläche der Kurve ausmachen.
Daher kann man solche Konfidenzintervalle so interpretieren, dass innerhalb dieser Wertgrenzen 95% aller geschätzten Werte zu liegen kommen werden, oder, anders ausgedrückt, dass man nur in 5% einen Fehler macht, wenn man sagt innerhalb dieses Wertebereiches liegt der wirkliche Wert.
[/raw]
Im Beispiel der Meta-Analyse ist also der aufgeführte Konfidenzbereich der Effektgrössen-Schätzung derjenige Bereich, in dem mit 95%iger Wahrscheinlichkeit der echte Wert zu liegen kommt. Weil in die Berechnung des Standard-Fehlers die Größe der zugrundeliegenden Studie eingeht, sind diese Konfidenzintervalle entsprechend unterschiedlich groß. Kleine Studien, wie die Pilotstudie von Yakir oder die Studie von Siebenwirth, haben sehr große Konfidenzbereiche, relativ große Studien wie die von Elli de Lange de Klerk haben kleine Konfidenzbereiche.
In der Grafik ist die Linie bei der OR von 1 durchgezogen. Das ist die Null-Effekt-Linie. Sie kennzeichnet den Wert, wo überhaupt kein Effekt vorhanden ist, nämlich bei einer OR von 1. Alles was links davon steht bezeichnet einen negativen Effekt, bei dem eine Studie Placebo als besser erscheinen lässt. Alles was rechts davon liegt, demonstriert einen Effekt. Wenn die Linie des Konfidenzintervalls die Null-Effekt-Linie schneidet, ist der Effekt der einzelnen Studie nicht sonderlich klar bzw. statistisch gesehen nicht signifikant. Man kann unmittelbar verstehen, dass dies von zwei Grössen abhängt: nämlich davon, wie groß der Effekt der Studie ist, und wie ausgezogen die Konfidenzintervalle sind bzw. wie groß die Studie ist. Dies ist eine andere Art und Weise, das zu sagen, was ich in meinem Blog über statistische Power („Die Magie der Statistik“) bereits gesagt habe: Ob eine Studie signifikant wird, hängt von der Effektgröße und der Studiengröße ab. Wir sehen an der Grafik: nur wenige Studien sind unabhängig signifikant, weil sie große Effektstärken aufweisen.
Nun sehen wir unterhalb der einzelnen Studien einen sog. „Diamanten“. Dies ist der Schätzer für die gesamte, gemittelte Effektgröße aller oben abgebildeten Studien und sein Konfidenzbereich, nebenan auch in Klammern angegeben. Schneidet dieser die Linie nicht, enthält also der Konfidenzbereich nicht den Wert „1.0“ oder kleiner, dann ist er statistisch signifikant. Wir sehen zwei solcher summarischer Schätzer: oben einen für die Studien mit kontinuierlichem Outcome mit einer signifikanten Odds Ratio von 1.45, unten einen für die Studien mit dichotomem Outcome mit einer Odds Ratio von 1.80 (mit einem grösseren Konfidenzbereich, aber auch nicht die Linie schneidend und daher signifikant). Und schließlich noch eine gesamte Schätzung für alle Studien. Diese liegt mit einer Odds Ratio von 1.53 und einem Konfidenzbereich, der 1 nicht mit einschließt ebenfalls im signifikanten Bereich.
Links daneben lesen wir „RE Model“. Das bedeutet: Hier wurde ein statistisches Modell angewandt, das ein Modell zufälliger Effekte annimmt („random effects model“, daher RE model). Das bedeutet folgendes: Man könnte ja auf die Idee kommen, dass alle Studien, die eine bestimmte Frage untersuchen am Ende auf einen „wahren“ Wert konvergieren. Das würde statistisch gesehen bedeuten: jede Studie kann ausgedrückt werden als ein gemessener Wert plus eine Abweichung von diesem wahren Wert, ein sog. „Fehler“. Diese Annahme ist in aller Regel problematisch, weil wir nicht wissen, ob sie wirklich stimmt. Daher ist eine konservativere, und in vielen Fällen einleuchtendere Annahme, dass eine Meta-Analyse Werte schätzt, denen ein wirklicher Wert zugrunde liegt, zusammen mit einem Fehler, die aber alle noch um eine unbekannte, zufällige Schwankung um diesen wahren Wert herum variieren. Warum, das wissen wir nicht, aber wir vermuten, dass es solche Schwankungen gibt. Dies ist das Modell „zufälliger Effekte“. Es äußert sich darin, dass die Schätzung der Werte weniger präzise ist und ist also statistisch gesehen konservativer. Praktisch nimmt man ein solches Modell immer dann an, wenn man es mit einer sehr heterogenen Gruppe von Studien zu tun hat, wie dies ja hier der Fall ist. Durch die Anwendung eines „random effect“ Modells wie hier wird die Schätzung also konservativ und ist damit glaubwürdiger.
Soweit ist alles also gut: wir haben eine präzise Schätzung von mittleren Effektgrössen individualisierter Homöopathie gegen Placebo, die zeigen, dass homöopathisch behandelte Patienten etwa 53% bessere Heilungschancen haben als placebo-behandelte, was statistisch signifikant ist. Das ist nicht schlecht, finde ich. Aber was genau bedeutet das? Was sagt es aus?
Um uns besser orientieren zu können, transformieren wir diese OR [10] und erhalten ein approximiertes d = 0.235 oder d = 0.23. Das ist ein eher kleiner Effekt. Um ihn einordnen zu können stellen wir ihn in Relation. Stefan Schmidt hat eben eine grundlegende Einführung über die experimentellen Effekte der Parapsychologie vorgelegt [11]. Dort findet sich eine Zusammenfassung von Effektstärken (alle signifikant) von neueren Meta-Analysen innerhalb der Parapsychologie, die ich in Auszügen wiedergebe:
Tabelle 2 – Effektstärken parapsychologischer Standard-Experimentalparadigmata in neueren Meta-Analysen
| Paradigma [12] | Effektstärke d | p-Wert |
| Presentiment (Mossbridge 2012) | 0.21 | 2*10-12 |
| DMILS (Schmidt 2004) | 0.11 | 0,001 |
| Remote Staring (Schmidt 2004) | 0.13 | 0,01 |
| Attention Facilitation (Schmidt 2012) | 0.11 | 0,030 |
Wir sehen, die Effektgrösse, die Homöopathie gegenüber Placebo zeigt ist etwas grösser als die größte der parapsychologischen Effekte. Wie sieht es mit der klinischen Medizin aus? Da kommt uns eine vor kurzem publizierte Übersicht zu Hilfe, die die Effektgrößen psychiatrisch-pharmakologischer Interventionen mit denen aller möglicher medizinischer Standard-Prozeduren verglichen hat [13]. Ich gebe die dort beschriebenen Effektgrößen in Auszügen wieder:
Tabelle 2 – Effektgrössen von ausgewählten medizinischen Interventionen aus Meta-Analysen, zusammengestellt von [13] und auszugsweise entnommen; die unterschiedlichen Effektrössen für psychiatrische Interventionen kommen daher, dass in einem Satz Studien unterschiedliche Zielkriterien verwendet wurden und in diesen Meta-Analysen unterschiedlich verrechnet wurden: Rating-Angaben von Fragebögen oder klinischen Symptomenscores, oder Responderanalysen nach klinischen Kriterien
| Krankheitsbild | Effektgröße d |
| Blutdrucksenkung: | 0.54 |
| Kardiovaskuläre Ereignisse: | 0.16 |
| Prävention kardiovaskulärer Krankheit und Schlaganfall: | 0.06 bis 0.12 |
| chron. Herzversagen: | 0.11 |
| Rheumatoide Arthritis (Methotrexat): | 0.86 |
| Migräne akut: | 0.41 |
| präventiv: | 0.49 |
| Asthma: | 0.56 |
| COPD (chron. obstruktive Lungenerkrankung): | 0.36.; 0.20 |
| Diabetes/Metformin: | 0.87 |
| Hepatitis C: | 2.27 |
| Ösophagitis: (Protonenpumpeninhibitoren) | 1.39 |
| Colitis ulcerosa: | 0.44 |
| MS Verschlimmerung: | 0.34 |
| Brustkrebs (Polychemotherapie): | 0.24 |
| Antibiotika für Otitis: | 0.22 |
| für Cystitis: | 0.85 |
| Bei psychiatrischen Erkrankungen: | |
| Schizophrenie: | 0.30-0.43 (Responder) 0.51-0.52 (Rating) |
| Depression: | 0.32 (Rating) 0.24-0.30 (Responder) |
| Rückfallverhütung: | 0.53-0.92 (mit Lithium) |
| Zwangserkrankung: | 0.44 (Symptome) 0.53 (Response) |
| Bipolare Störung: | 0.40-0.53 (Symptome) 0.41-0.66 (Response) |
| Rückfallverhütung: | 0.37-1.12 |
| Panik: | 0.41 |
| Demenz: | 0.26-0.41 |
| ADHS: | 0.78 |
Wir sehen an dieser Vergleichstabelle zwei Dinge: erstens schwanken die Effektgrößen auch in der konventionellen Medizin enorm zwischen einer kleinen Effektgröße von d = 0.11 bei der Prävention von Herzversagen oder d = 0.06 bei der Prävention von Schlaganfall und sehr großen wie d = 2.27 bei Hepatitis C (allerdings nur wenige Studien). Im Median liegen die Effektgrößen bei d = 0.4. Das Ziel der Studie [13] war es herauszufinden, ob psychiatrische Interventionen mit konventionell-medizinischen vergleichbar sind. Sie sind es und haben allerdings ein etwas geringeres Schwankungsspektrum. Aber auch in der Psychiatrie gibt es relativ geringfügig wirksame Interventionen, wie etwa die Behandlung von Depressionen, wenn ein hartes Kriterium (hat ein Patient eine positive Reaktion auf die Therapie?) gefragt wird, oder in der Therapie von Demenz. Auch hier ist die mittlere Effektstärke mit d = 0.4 etwa der der konventionellen Behandlungen ebenbürtig.
Die Homöopathie nimmt sich also mit ihren d = 0.23 gar nicht so übel aus. Wir müssen bei der Interpretation folgendes berücksichtigen: Die Meta-Analyse von Mathie und Kollegen war bewusst so angelegt, dass die Schätzung der Effektgrößen konservativ erfolgte. Viele Studien gingen nicht in die Analyse ein, weil sie nicht den Kriterien entsprachen, eben genau um den Effekt nicht zu verdünnen oder aufzublähen. Und der Vergleich findet statt, wie mir ein Gutachter mal geschrieben hat „zwischen einem Placebo und einem anderen Placebo“, denn pharmakologisch enthalten die homöopathischen Arzneimittel „nichts“, jedenfalls nichts Feststellbares und Wägbares. Und insofern ist dieses Ergebnis wissenschaftlich gesehen sensationell. Denn es hätte gar nicht auftreten dürfen.
Wird es die Debatte um die Homöopathie beenden? Wissen wir jetzt mit Sicherheit, dass Homöopathie kein Placebo ist? Nein, ich glaube nicht. Zum einen ist eine Meta-Analyse ein Bild in einem dynamischen Geschehen. Zum anderen ist das Ergebnis von so vielen Vorannahmen abhängig, vom Ein- und Ausschluss von Studien etwa, dass eine andere Arbeitsgruppe, die mit dem gleichen Studienmaterial aber mit leicht veränderten Kriterien oder Prozeduren zu anderen Ergebnissen kommen könnte, wie das schon oft in anderen Bereichen geschehen ist. Denn, das übersehen die meisten: Meta-Analysen sind aus meiner Sicht Forschungsinstrumente, die uns helfen neue Wege zu finden und abzuklären, ob wir in einem pragmatischen Sinne bereits ausreichend viel wissen und wie dieses Wissen, kumulativ, zu beziffern ist. Wie dieses Wissen dann einzuordnen und zu bewerten ist, ist eine ganz andere Frage. Die Beantwortung hängt davon ab, wie groß ein Effekt sein muss, damit er uns interessiert, welche anderen Optionen zur Therapie es gibt, wie kostspielig sie sind, wie stark mit Nebenwirkungen behaftet, usw.
Die Meta-Analyse war ursprünglich eine Erfindung von Psychologen um die Streitfrage zu klären, ob Psychotherapie wirkt oder nicht [14, 15]. Sie hat mindestens damals einen konstruktiven Dialog angeregt. Die ursprüngliche Frage ist eher noch komplexer geworden, denn beantwortet. Man konnte sagen: irgend etwas an der Psychotherapie scheint zu funktionieren. Aber was genau? Bei wem genau? Bei welcher Methode? Und warum? Solche Fragen werden normalerweise meta-analytisch durch Moderatorenanalysen untersucht und dann in weiteren Prozessforschungsstudien (siehe Box Moderatoranalyse).
[raw]
In der Analyse von Mathie und Kollegen gab es keine Heterogenität. In unserer eigenen Meta-Analyse zu Achtsamkeit bei Kindern [16] gab es große Heterogenität. Wir konnten sie aufklären, indem wir feststellten, dass die Studien mit der größten Effektstärke alle von einer Arbeitsgruppe kamen, die ein besonders intensives Training bei eher älteren Jugendlichen untersucht hatte. Auf diese Art und Weise tragen dann Meta-Analysen auch dazu bei, die Bedeutung einzelner Variablen für den untersuchten Effekt aufzuklären, vorausgesetzt man hat die Variable vorher erfasst und hat ausreichend viele Studien im Portfolio, um solche Analysen zu rechnen. Man kann auch die Analyse von Lüdtke und Rutten [4] als eine nachgeholte Moderator-Analyse zur Meta-Analyse von Shang [3] betrachten, die zeigt, dass das Ergebnis von Shang nicht robust genug ist, um als wissenschaftlicher Tatbestand durchzugehen. Denn das Ziel von Moderator-Analysen ist es, die Robustheit der Analyse gegen Verletzung von Annahmen oder unter verschiedenen Szenarien zu dokumentieren.
[/raw]
All diese zusätzlichen Fragen werden heute, 35 Jahre nach der ursprünglichen Analyse von Smith und Glass, noch heiß diskutiert. Kann also die Analyse von Mathie klären, ob Homöopathie Placebo ist? Nein, kann sie nicht. Aber sie legt ein paar gute Argumente vor die zeigen, dass die Frage nicht einfach vom Tisch ist. Denn wenn dem so wäre, dann hätten wir hier nicht unbedingt eine signifikante Effektstärke erwartet. Aber warum sollte das so sein? Wir können wir uns das erklären? Und: sollte uns das interessieren? All diese Fragen kann die Analyse nicht beantworten.
Ich meine: sie sollten uns interessieren. Wenn die Analyse eine ganz normale, konventionell-medizinische Behandlungsmethode zum Gegenstand gehabt hätte, bei der man meint, den zugrundeliegenden pharmakologischen Mechanismus zu kennen und die in jedem Krankenhaus verwendet wird, wäre es höchstwahrscheinlich zu einem Kommentar von der Sorte gekommen: „Nun ja, so stark, wie wir uns das erhofft hatten, ist der Effekt nun auch nicht. Aber er ist doch ganz klar signifikant und immer noch besser als Placebo.“ Nun ist die Intervention aber zwar bekannt, aber umstritten, und wir haben überhaupt keine Idee, wie sie funktionieren könnte. Genau deswegen sollte uns das Verfahren, die Homöopathie, und das Ergebnis der Analyse beginnen zu interessieren.
Aber dazu sind viele andere Schritte nötig. Vor allem ein Diskurs darüber, was einen Befund wissenschaftlich interessant macht. Ich finde, die Analyse eröffnet zumindest den Dialog dazu und hat auf jeden Fall einen Befund robust dokumentiert, der all diejenigen, die noch nicht glauben, wir wüssten schon alles, interessieren müsste. Denn wie kann es sein, das etwas, das nicht da ist, gegenüber etwas, das nicht da ist, einen klaren, statistisch signifikanten und auch klinisch nicht uninteressanten Effekt erzeugt? Was uns die Meta-Analyse sagt ist, dass dieser Effekt in weniger als einem von 1000 Fällen per Zufall auftritt. Das schließt Zufall nicht aus, macht ihn aber nicht sonderlich attraktiv als Erklärung. Was kann uns einen solchen Effekt erklären?
Die Meta-Analyse eröffnet also eher Fragen, als dass sie welche beantwortet. Und Fragen zu stellen, war schon immer der Königsweg der Wissenschaft. Nicht, zu glauben, alle Fragen schon beantwortet zu haben. Das ist die Methode der Dogmatik und der Religion. Insofern ist die Meta-Analyse eine wissenschaftliche Methode. Sie produziert meistens mehr Fragen, als sie beantwortet, auch wenn sie dabei einige Fragen, die man vorher gestellt hat, beantwortet. Jetzt wissen wir: individualisierte homöopathische Therapie ist statistisch gesehen eher nicht Placebo-Therapie – jedenfalls bei der Datenlage, die wir im Moment haben. Aber das lässt uns eigentlich ratlos zurück. Denn jetzt müssen wir uns vielleicht überlegen, wie das sein kann. Oder neue Studien machen. Oder beides. Es hört einfach nie auf…
Darum sollten die, die sich für die endgültige Klärung von Fragen interessieren Priester werden, nicht Wissenschaftler.
Quellen und Hinweise
- Mathie, R. T., Lloyd, S. M., Legg, L. A., Clausen, J., Moss, S., Davidson, J. R., et al. (2014). Randomised placebo-controlled trials of individualised homoeopathic treatment: sytematic review and meta-analysis. Systematic Reviews, 3(142). doi:10.1186/2046-4053-3-142 [online verfügbar]
- Walach, H., Gaus, W., Haeusler, W., Lowes, T., Mussbach, D., Schamell, U., et al. (1997). Classical homoeopathic treatment of chronic headaches. A double-blind, randomized, placebo-controlled study. Cephalalgia, 17, 119-126.
- Shang, A., Huwiler-Münteler, K., Nartey, L., Jüni, P., Dörig, S., Sterne, J. A. C., et al. (2005). Are the clinical effects of homeopathy placebo effects? Comparative study of placebo-controlled trials of homoeopathy and allopathy. Lancet, 366, 726-732.
- Lüdtke, R., & Rutten, A. L. B. (2008). The conclusions on the effectiveness of homeopathy highly depend on the set of analyzed trials. Journal of Clinical Epidemiology, 61, 1197-1204.
- Cucherat, M., Haugh, M. C., Gooch, M., Boissel, J. P., & HMRAG Group. (2000). Evidence of clinical efficacy of homeopathy. A meta-analysis of clinical trials. European Journal of Clinical Pharmacology, 56, 27-33.
- Linde, K., Clausius, N., Ramirez, G., Melchart, D., Eitel, F., Hedges, L. V., et al. (1997). Are the clinical effects of homoeopathy placebo effects? A meta-analysis of placebo controlled trials. Lancet, 350, 834-843.
- Mathematisch präzise wird die Streuung folgendermassen ermittelt: Man bildet erst die Differenzen der einzelnen Werte vom Mittelwert und quadriert sie; dadurch verschwinden alle negativen Vorzeichen. Dann summiert man diese sog. Abweichungsquadrate auf und mittelt sie, d.h. teilt sie durch die Anzahl der Differenzen oder Werte, die in die Rechnung eingegangen sind. Das bedeutet: auch hier findet wieder eine Standardisierung statt auf die Anzahl der Werte; so werden Streuungen von Werte in großen und kleinen Stichproben vergleichbar. Um dann wieder auf die ursprüngliche Metrik zu kommen – wir haben ja vorher quadriert – wird nun die Wurzel aus diesem Wert gezogen. Der so gefundene Wert heißt „Standardabweichung“. Der Ausgangswert, also die Summe der standardisierten und quadrierten Abweichungen vom Mittelwert heißt „Varianz“.
- Hasselblad, V., & Hedges, L. (1995). Meta-analysis of screening and diagnostic tests. Psychological Bulletin, 117, 167-178.
- Chinn, S. (2000). A simple method for converting an odds ratio to effect size for use in meta-analysis. Statistics in Medicine, 19, 3127-3131. Eine odds ratio wird erst logarithmiert. Dann kann man sie in eine Effektgrösse d konvertieren, indem man die logarithmierte Odds Ratio durch 1.81 teil, ebenso die Standardabweichungen. Dies approximiert die Effektgrösse d, weil die logistische Verteilung der Standardnormalverteilung ziemlich entspricht und als Projektion als Standardnormaldeviate überall ausser an den äusserten Rändern linear ist, mit einer Varianz von pi2/3-2, was 1.81 ist. Dadurch gewinnt sind die Konfidenzintervalle kleiner, weil die statistische Mächtigkeit zunimmt.
- Über die Prozedur, wie unter [9] beschrieben: wir nehmen den natürlichen Logarithmus von 1.53; Ergebnis: 0.425. Wir dividieren dies durch 1.81: d = 0.235
- Schmidt, S. (2014). Experimentelle Parapsychologie – Eine Einführung. Würzburg: Ergon, S. 99.
- Presentiment-Studien sind solche, bei denen über ein physiologisches Maß erforscht wird, ob Menschen angsteinflössende Bilder erahnen, bevor sie gezeigt werden. DMILS-Studien sind solche, bei denen jemand die autonome Erregung einer anderen Person über die Distanz beeinflusst. Remote Staring sind Studien, bei denen eine Person das Bild einer anderen auf einem Bildschirm anschaut und bei der angeschauten Person die autonome Erregung gemessen wird. Und bei Attention Facilitation geht es darum, dass eine Gruppe von Personen über die Distanz hinweg einer anderen Person in Zufallsfolge helfen soll, sich auf einen Stimulus zu konzentrieren.
- Leucht, S., Hierl, S., Kissling, W., Dold, M., & Davis, J. M. (2012). Putting the efficacy of psychiatric and general medicine medicatin into perspective: review of meta-analyses. British Journal of Psychiatry, 200, 97-106.
- Smith, M. L., Glass, G. V., & Miller, T. I. (1980). The Benefits of Psychotherapy. Baltimore: Johns Hopkins University Press.
- Matt, G. E. (1989). Decision rules for selecting effect sizes in meta-analysis: a review and reanalysis of psychotherapy outcome studies. Psychological Bulletin, 105, 106-115.
Matt, G. E. (1997). What meta-analyses have and have not taught us about psychotherapy effects: A review and future directions. Clinical Psychology Review, 17, 1-32.
Wittmann, W. W., & Matt, G. E. (1986). Meta-Analyse als Integration von Froschungsergebnissen am Beispiel deutschsprachiger Arbeiten zur Effektivität von Psychotherapie. Psychologische Rundschau, 37, 20-40. - Zenner, C., Herrnleben-Kurz, S., & Walach, H. (2014). Mindfulness-based interventions in schools – a systematic review and meta-analysis. Frontiers in Psychology; 5: Art. 603. doi:10.3389/fpsyg.2014.00603 [online verfügbar]